~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 通常より20%増量されて960mL入ったジュースが売られています。元は何mL入りで売られていましたか。
(2) ある小学校の児童500人のうち,40%が学校からの距離が300m以内のところに住んでおり,そのうちの15%が100m以内のところに住んでいます。学校から100mより遠く,300m以内のところに住んでいる人の割合は何%ですか。
(3) まこさんは家を駅に向かって歩き出しました。608m歩いたところ,駅までの道のりは残り36%となりました。家から駅までは何mですか。
(4) と 0.55 ではどちらが大きいですか。
2 次の表は,ある果物の都道府県別の収穫量を表しています。
| 北海道 | 山梨 | 長野 | 福島 | |
| 収穫量(トン) | 500 | 240 | 150 | 70 |
北海道の収穫量を基準としたとき,山梨,長野,福島の合計の収穫量の割合はいくつになりますか。
10点
3 みかさんは算数の時間に三角形の面積について学習しました。
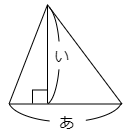
図のような三角形の面積は「あ×い÷2」で求めることができます。
次の各問いに答えなさい。
10点×3=30(点)
(1) 図の「あ」の長さを4cmとします。このとき次の表を完成させなさい。また,「い」の長さが2倍,3倍,4倍…になると面積はどうなるか説明しなさい。
| 「い」の長さ(cm) | 1 | 2 | 3 | 4 | 5 |
| 面積(cm²) |
(2) 今度は図の「い」の長さを4cmとします。このとき次の表を完成させなさい。また,「あ」の長さが2倍,3倍,4倍…になると面積はどうなるか説明しなさい。
| 「あ」の長さ(cm) | 1 | 2 | 3 | 4 | 5 |
| 面積(cm²) |
(3) 最初に「あ」を2cm,「い」を3cm としておきます。ここから「あ」と「い」の長さを同時に2倍,3倍,4倍,…と変化させたときの面積を計算して表を完成させなさい。更に,「あ」と「い」の長さを同時に2倍,3倍に4倍…というように変化させたとき,面積はどのような規則で大きくなっていくかを,その規則を説明しなさい。
| 「あ」と「い」の倍率 | 1倍 | 2倍 | 3倍 | 4倍 | 5倍 |
| 面積(cm²) |
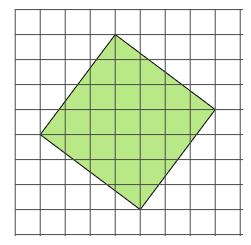
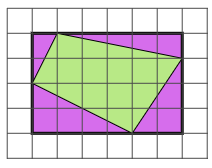
4 次の方眼紙は,1マスがたて・横ともに1cmの正方形です。次の各問いに答えなさい。
10点×2=20(点)
(1) 次の緑色の四角形の面積を求めなさい。
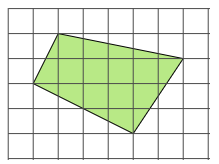
(2) 図の緑色の四角形は正方形です。この正方形の1辺の長さを求めなさい。