
~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) $\dfrac7{12}-\dfrac13$ を小数で表しなさい.
こたえ
$\dfrac7{12}-\dfrac13=\dfrac{7-4}{12}=\dfrac3{12}=\dfrac14$
$\dfrac AB$ は,$A\div B$ を意味しますから
1÷4=0.25
答えは 0.25
(2) 6.23×0.15-6.23×0.14
こたえ
工夫をして計算しましょう。分配の決まりが使えそうです。
6.23×0.15-6.23×0.14=6.23×(0.15-0.14)
=6.23×0.01=0.0623
答えは 0.0623
(3) 508, 610, 622, 596 の平均を求めなさい.
こたえ
基準値を最も小さい数の508にすると引き算が大変です。基準値を500にして,計算を簡単にしましょう。
基準値500からのずれは順に
8, 110, 122, 96
です。この4つの数の平均は
(8+110+122+96)÷4=336÷4=84
よって, 500+84=584
答えは 584
(4) たて2500mm,横40cmの長方形の面積は何m2ですか。
こたえ
求める単位がm$^2$なので,たて,横をメートルに直してから計算しましょう。
たて:2500㎜=2.5m
横:40cm=0.4m
よって 2.5×0.4=1
答えは 1m2
2 次の分数はある規則(きそく)に従って並んでいます。50番目の分数は何ですか。
\[\dfrac11,\ \dfrac12,\ \dfrac22,\ \dfrac13,\ \dfrac23,\ \dfrac33,\ \dfrac14,\ \dfrac24,\ \cdots\]
10点
こたえ
次のようにグループに分けましょう。
\[\dfrac11\Big|\ \dfrac12,\ \dfrac22\Big|\ \dfrac13,\ \dfrac23,\ \dfrac33\Big|\ \dfrac14,\ \dfrac24,\ \cdots\]
この規則を考えてみると
①1番目のグループには1個,2番目のグループには2個,3番目のグループには3個,というように分数が含まれています。
②1番目のグループの分母は1,2番目のグループの分母は2,3番目のグループの分母は3,となっています。
50番目の分数が何であるかを知るには,それが何番目のグループの何番目の分数かを調べればわかります。
1+2+3+4+5+6+7+8+9=45
1+2+3+4+5+6+7+8+9+10=55
よって9番目のグループまでには45個の分数があり,10番目のグループまでには55個の分数がありますから,50番目の分数は10番目のグループの5番目です。10番目のグループの分母は10ですから求める分数は $\dfrac5{10}$ です。
答えは $\dfrac5{10}$
3 あきこさんは,60リットル入る水そうに水を入れて,満水になったらすぐに水を排水(はいすい)しました。次のグラフはそのときの様子を表しています。
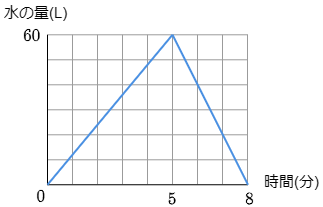
次の問いに答えなさい。
10点×3=30(点)
(1) 水そうに水を入れているとき,毎分何リットルの水が入っていますか。
こたえ
5分間で60リットルの水が入りましたから,
60÷5=12
答えは 毎分12リットル
(2) 水そうの水を排水するとき,毎分何リットルの水が排水されていますか。
こたえ
3分間で60リットルの水は排水されましたから
60÷3=20
答えは 毎分20リットル
(3) 水を入れ始めてから4分後,水そうにたまっている水の量は何リットルですか。
こたえ
(1)で1分間当たりに入る水の量が12リットルでしたから,4分では
12×4=48
答えは 48リットル
4 100個のおはじきをできるだけ多く使い,次の規則(きそく)に従って図のように正三角形に並べます。
- 各辺には同じ個数のおはじきを等間隔(かんかく)に並(なら)べます。
- 各頂点にはおはじきを置きます。
次の各問いに答えなさい。
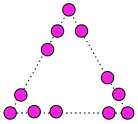
10点×2=20(点)
(1) おはじきは何個あまりますか。
こたえ
三角形の辺に同じ個数だけ並べるのですから,3の倍数となります。100以下の3の倍数の中で,100に最も近い数を探しましょう。
100÷3=33あまり1
答えは 1個
(2) 三角形の1辺に並べるおはじきの個数は何個ですか。
こたえ
頂点にはおはじきを置くことに注意です。1つの頂点は2つの辺のはしの点となっていますから,単純(たんじゅん)に(1)で求めたおはじきの個数の3分の1ではありません。頂点を2重に数えなくてもよいような上手な数え方を考えましょう。
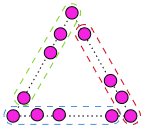
例えば図のように数えると,どの点線の枠内にも33個のおはじきがあり,それにもう1個,頂点の分がありますから合計34個です。
答えは 34個

