~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 17−(23−14)
カッコがあるときはカッコ内が優先(ゆうせん)です。
(2) 421×7.17+421×2.83
工夫をして計算しましょう。分配の決まりが使えそうです。
(3) 千の位までの概数(がいすう)が10000になる整数の範囲を求めなさい。
千の位までの概数ですから百の位を四捨五入したのです。
(4) たて10cm,横12cm,高さ50cmの容器に,5260mL(ミリリットル)の水を入れました。あと何リットル入れることができますか。ただし,容器の底や側面の厚みは考えません。
まずこの容器の容積を計算しましょう。1辺が10cmの立方体の体積が1リットルでした。mL(ミリリットル)の「m」は1000分の1を意味します。
2 5人が算数のテストを受けたところ,平均点は82点でした。最高点を除く4人の平均点は80点です。最高点の人は何点でしたか。
10点
平均点からはそれぞれの人が何点取ったかはわかりませんが,合計点なら計算で求めることができます。
3 次の各問いに答えなさい。
10点×3=30(点)
(1) 3で割るとあまりが1になる整数のうち,50に最も近い数は何ですか。
3で割るとあまりが1となる整数は,前回と前々回で見てきたように
(3の倍数)+1
です。3の倍数の中で50に最も近い整数を探しましょう。
(2) 7で割るとあまりが1となる整数のうち,100に2番目に数は何ですか。
(1)と同じで,7で割るとあまりが1となる整数は
(7の倍数)+1
と表されます。「2番目に近い」ということころに注意してください。
(3) 3で割っても7で割ってもあまりが1となる整数のうち,200に最も近い数は何ですか。
3で割っても7で割ってもあまりが1となる数は,「(3と7の最小公倍数)+1」で表されます。これらは規則的(きそくてき)に並んでいます。よって(3と7の最小公倍数)の倍数のうちで,200に最も近い数を探してみましょう。
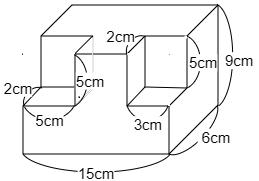
4 たて6cm,横15cm,高さ9cmの直方体から,図のように2つの直方体を取りのぞいた立体があります。
次の各問いに答えなさい。
10点×2=20(点)
(1) この立体の体積は何cm3ですか。
ひさしぶりの体積です。直方体の体積は,(たて)×(横)×(高さ) で計算します。
(2) この立体の表面全体の面積は何cm2ですか。
たくさん面があって計算が大変ですが,考え方を工夫することで,あっという間に求めることもできます。詳しくは 課題⑦ とその解説を見てください。(解説は課題⑦の返却された答案にリンクがあります。)