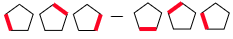～解き始める前に～
答案の提出方法，注意点はこちら をご覧ください。
１ 次の計算をしなさい。
10点×4=40(点)
(1) $\dfrac{109}{20}+\dfrac{23}{20}-\dfrac35$
まずは $\dfrac{109}{20}$ と $\dfrac{23}{20}$ を帯分数にしましょう。3つの分数を計算するときは，3つとも同じ分母で通分するのではなく，2つずつ計算していくと計算の負担(ふたん)が減ります。1つ計算が終わるごとに，約分をすべきかどうか検討(けんとう)します。
(2) $\dfrac18$ を小数で表しなさい。
例えば1L(リットル)の水を8人で等しく分けるとき，1人がもらえる量は1Lの $\dfrac18$ ですが，これが何Lかを考えることと，この問題は同じです。
(3) 301.857÷421
(4) たて4500㎜，横0.0061kmの長方形の面積は何m2ですか。
求める単位はm$^2$ なので，長さをmになおしてから計算しましょう。
２ 2つの数AとBがあり，それぞれ十の位までの概数(がいすう)で表すと，Aは60，Bは100となります。またAは9の倍数で，AとBを足すと10の倍数となります。AとBの数をそれぞれ求めなさい。
10点
十の位までの概数の場合は一の位を四捨五入しています。A，Bそれぞれがとる値のはんいを調べましょう。次にAの値が9の倍数という条件から，Aの値が決定します。そのAの値とBを足すと10の倍数になるのですから，Bの値も決定します。
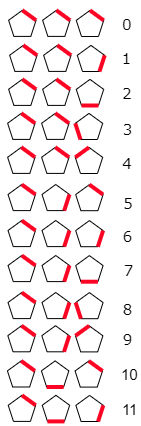
３ 次のように，五角形と赤色の線で数字を表すことを考えます。
次の各問いに答えなさい。
10点×3=30(点)
(1) 表せる数字の中で，最も大きな数字は何ですか。
最初の0, 1, 2, 3, 4 を見て，赤色の線の位置との対応を理解しましょう。
私たちがふだん使っている数は10を1つのかたまりとして考える数字で，
1の位，10の位，100(10×10)の位，1000(10×10×10)の位
となっています。例えば4217という数字は
10×10×10が4個
10×10が2個
10が1個
1が7個
という風に考えて
4000＋200＋10＋7
と表せます。一方，この問題の数字は5を1つのかたまりとして考えますから
1の位，5の位，25(5×5)の位
となっています。（このような数の表し方を5進法といいます。)
(2) 83を表す図をかきなさい。
83は25×○＋5×△＋1×☆で表すとどうなるでしょうか。
(3) 次の計算結果を数字で答えなさい。
それぞれの記号が表す数字が何かを求めて引き算しましょう。
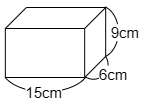
４ 図のような直方体がたくさんあります。
次の各問いに答えなさい。
10点×2=20(点)
(1) この直方体を並べて1つの立方体を作ります。出来上がった立方体の1辺の長さは何cmですか。
立方体はすべての面が正方形の六面体です。つまりどの辺の長さも同じになります。
(2) (1)で作った立方体の体積は何cm3ですか。
この立方体を作るために何個の直方体を使いましたか？
