
1 次の計算をしなさい。
10点×4=40(点)
(1) 53813−451013
こたえ
813 から 1013 は引けませんから,53を52+1にしてから計算します。
53=52+1=52+1313。よって 1313+813=2113。
従って問題は 52+2113−451013 と同じになりますから,52-45=7,2113−1013=1113。
答えは 71113_
(2) 43.61÷623
こたえ
小数点の位置に気をつけましょう。
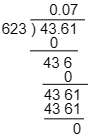
答えは 0.07
(3) 1001×999 (計算を工夫して求めなさい。)
こたえ
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。
1000=1000+1 ですから1001×999=(1000+1)×999 分配の決まりより1001×999+1×999 1000×999=999000 で,1×999=999 ですから,999000+999=999999。
答えは 999999
(4) 1辺の長さが10cmの立方体の容器に,容積が0.25dLの計量カップで水を入れていくとき,何回入れると満杯になりますか。
こたえ
1辺が10cmの立方体の容器は1000cm3 で,これは1Lです。さらに1Lは10dLです。よって10÷0.25=40 こたえは 40回
2 ある地方にはA,B,Cの3つの都市があり,これらの都市の人口について調査をしたところ,次のようになりました。
A市は千の位までの概数で1万4千人、B市は百の位までの概数で6700人,C市は一万の位までの概数で2万人でした。
この地方の人口として考えられるのは何人以上何人以下ですか。
10点
こたえ
A市は千の位までの概数で1万4千人ですから,13500人以上14499人以下です。
B市は百の位までの概数で6700人ですから,6650人以上6749人以下です。
C市は一万の位までの概数で2万人ですから,15000人以上24999人以下です。
以上により,最も少ない場合で,13500+6650+15000=35150(人) 最も多い場合で14499+6749+24999 これは計算が大変なので次のように計算しましょう。(14500−1)+(6750−1)+(25000−1)= 14500+6750+25000−1−1−1= 46250−3= 46247 答えは 35150人以上,46247人以下
3 あいさんとみかさんが,夏休みについて話しています。
あい「もうすぐ夏休みね。夏休みはどこかに行く予定はあるの?」
みか「飛行機に乗って東京のおばあちゃんのところに遊びに行く予定よ。」
あい「へえ,そうなんだ。私も飛行機に乗ったことがあるけど,空港って広いからなんだか疲れちゃった。」
みか「そうね。でも空港には動く歩道があるから助かるわ。」
あい「床に設置されたエスカレーターみたいなやつね。」
みか「そう。あの動く歩道ってどれくらいの速さなのかな。」
あい「ちょっと調べてみましょう。」
あいさんとみかさんは,インターネットを使って動く歩道について調べました。
みか「だいたい1分間に40mくらい進むみたいね。」
あい「なるほど,じゃあ動く歩道の長さが60mのときは,だいたい( ア )秒で動く歩道を渡り切ることができるわね。
みか「もし歩道の上でも歩いたら,もっと早く渡り切ることができるわ。」
あい「そうね,私たちの歩く速さがだいたい毎分80mよ。」
みか「すると,動く歩道の上でも歩き続けるとすれば,動く歩道上では1分間に( イ )mだけ進むことができるわね。」
あい「そしたら動く歩道の長さがさっきと同じ60mだとすれば,( ウ )秒で渡り切ることができるわ。」
この会話を元にして,次の問いに答えなさい。
10点×3=30(点)
(1) ( ア )に入る数字を答えなさい。
こたえ
求める単位は秒なので気をつけてください。
1分間に40m進むので,60m進むためには 60÷40=1.5(分)かかります。0.5分は1分の半分なので30秒。よって60+30=90(秒)
答えは 90秒
(2) ( イ )に入る数字を答えなさい。
こたえ
動く歩道が1分間に40m,歩く速さが1分間に80mですから,動く歩道上でも歩くとすれば,1分間に40+80=120(m)進むことができます。
答えは 120m
(3) ( ウ )に入る数字を答えなさい。
こたえ
1分間に120m進むとき,60m進むのにかかる時間は,60÷120=0.5(秒)
答えは 30秒
4 次の角度を求めなさい。
10点×2=20(点)
(1) 次の2つの緑色の角度の合計は何度ですか。

10点
こたえ
三角形の3つの角の合計が180°であることが基本となりますが,三角形の2つの角の合計は,残りの角の外側の角と等しいことを利用するとかんたんです。
下の図で,緑色と水色の角の合計は,赤色の角と等しくなります。
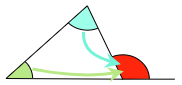
この関係がどうして成り立つか説明しましょう。
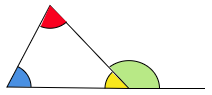
まずどんな三角形も3つの角の和は180°ですから,図の赤,青,黄の3つの角の合計は180°です。一方,黄と緑の角の合計は直線となりますから180°です。つまり
赤+青+黄=黄+緑
よって 赤+青 = 緑
となるのです。
それでは問題の図を見てみましょう。黄色の三角形に注目してください。
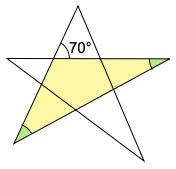
従って先ほど確認したことから,2つの緑の角の合計は70°です。
答えは 70°
(2) 次の5つのむらさき色の角度の合計は何度ですか。
10点

こたえ
これは大変有名な問題です。(1)と同じことを,別の三角形を使って2つの角度の合計と等しい場所を考えましょう。
まずは(1)と同じ三角形を考えると,下の図の2つの緑の角の合計が青色になります。
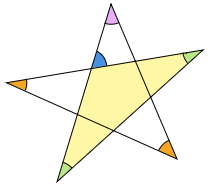
次に別の三角形に注目すると,2つのオレンジ色の角の合計が赤色になります。
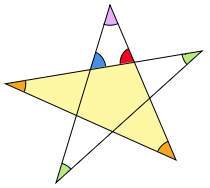
従って5つのむらさき色の角が,1つの三角形の3つの角に集まってきました。
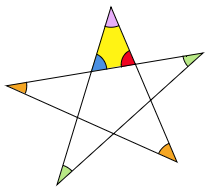
答えは 180°

