1 次の計算をしなさい。
10点×4=40(点)
(1) $7-2\dfrac25+3\dfrac25$
こたえ
帯分数というのは「+」を省略した数字の表現方法です。例えば $2\dfrac25$ というのは $2+\dfrac25$ という意味です。すると問題は\[7-\left(2+\dfrac25\right)+\left(3+\dfrac25\right)\]を意味します。この式をさらに説明すると「7から2と $\dfrac25$ を引いて,3と $\dfrac25$ を足したもの」となります。分数だけに注目すると,$\dfrac25$ は引かれたすぐあとに足されれもしますから,結局 $\dfrac25$ は最初からなかったも同然です。よって $7-2+3=8$
答えは 8
(2) $7.17\times8.3$
こたえ
小数点の位置に気をつけましょう。
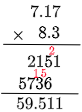
答えは 59.511
(3) $0.0623\times4+0.0623\times96$
こたえ
$0.0623\times4+0.0623\times96=0.0623\times(4+96)$
よって,$0.0623\times100=6.23$
答えは 6.23
(4) たて120cm,横50cm,高さ80cmの直方体の体積は何m3ですか。
こたえ
$\rm m^3$ で答えなければならないので,各辺の長さをm(メートル)に変えてから計算しましょう。120cm=1.2m,50cm=0.5m,80cm=0.8mですから,求める体積は 1.2×0.5×0.8=0.48
答えは 0.48 m3
2 ある町の人口は,千の位の概数で1万3千人でした。この町の人口は何人以上何人以下ですか。
10点
こたえ
千の位の概数で1万3千人ですから,この町の人口は12500人以上,13500人未満です。「13500人未満」は「13499人以下」と同じです。
答えは 12500人以上,13499人以下
3 ある小学校の5年生は1組から3組まであります。このたびクラス対抗の運動会が行われることになりました。種目は綱引き,ドッジボール,玉入れです。下の表は,各競技の結果で,勝ちは⚪︎,負けは×,引き分けは△で表されています。表はたてが「〜は」で,横が「〜に」を表します。例えば,綱引きにおいて,1組は2組に勝ち,2組みは1組に負けたことがわかります。得点は,勝つと2点,負けると0点,引き分けは1点です。
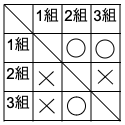
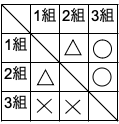
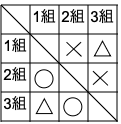
次の問いに答えなさい。
10点×3=30(点)
(1) 玉入れにおいて,各組の点数は何点ですか。
こたえ
1組:0+1=1(点)
2組:2+0=2(点)
3組:1+2=3(点)
よって 1組1点,2組2点,3組3点
(2) 総合優勝したのは何組ですか。またその組の点数は何点ですか。
こたえ
1組
綱引き :2+2=4(点)
ドッジボール:1+2=3(点)
玉入れ :0+1=1(点)
合計 4+3+1=8(点)
2組
綱引き :0+0=0(点)
ドッジボール:1+2=3(点)
玉入れ :2+0=2(点)
合計 0+3+2=5(点)
3組
綱引き :0+2=2(点)
ドッジボール:0+0=0(点)
玉入れ :1+2=3(点)
合計 2+0+3=5(点)
よって総合優勝したのは 1組 で,点数は 8点
(3) (2)で優勝した組を除いた残りの組は,総合得点が同点だったので,玉入れでカゴに入れた玉の多い組を2位にすることにしました。1組対2組は35対36,2組対3組は31対28,3組対1組は40対40でした。総合2位の組は何組ですか。
こたえ
優勝したのは1組ですから,2位と3位は2組と3組です。よって2組と3組の玉の数を数えましょう。
2組:36+31=67(個)
3組:28+40=68(個)
よって3組の方が玉が1個だけ多いですから,2位は 3組 です。
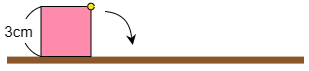
4 (1) 次の図は1辺の長さが3cmの正方形です。この正方形を,図のような線の上をすべらないように転がします。図の黄色い点が,ふたたび元の右上の位置に来るまで回転するとき,黄色い点が動いてできる線をコンパスを使ってかきなさい。
10点
こたえ
まずは転がったあとの正方形の図をかいて,黄色の点がどこに移ったのか考えましょう。黄色の点が動いてできる曲線は円の一部になりますから,コンパスを使ってかいていきます。
答えは,図の水色の線です。
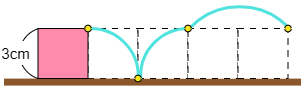
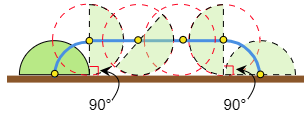
(2) 次の図は直径の長さが6cmの半円です。この半円を,図のような線の上をすべらないように転がします。直径が,ふたたび線の位置に来るまで回転するとき,半円の中心(黄色い点)が動いてできる線をコンパスと定規を使ってかきなさい。ただし,円周の部分の長さ(赤色の曲線部分)は 9.4cm とします。
10点
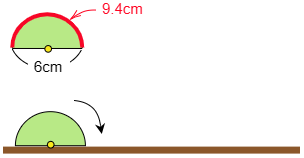
こたえ
(1)と同じように,半円が転がったあとの様子をあらかじめかいておきましょう。そして,黄色の円の中心がどこに移ったかを考えてコンパスと定規でかいていきます。
答えは,図の青色の線です。