～解き始める前に～
答案の提出方法，注意点はこちら をご覧ください。
１ 次の計算をしなさい。
10点×4=40(点)
(1) 527−247
27−47 は計算できませんから，527 を仮分数にするのですが，5を全部分数にする必要はありません。1は 77 と同じですから
5=4+1=4+77
というように1だけ仮分数にしてやりましょう。
(2) 2.74×14
最初は小数点を無視して 274×14 を計算します。計算できたら右から2番目に小数点を打ちます。
(3) 63−(24÷6÷2)×3
この問題は注意点が2つあります。
①たし算・引き算よりかけ算・わり算が優先です。
②わり算が連続するときは左から順に計算します。
(4) 64÷8÷4÷2
(3)と同じで，わり算が連続しています。この連続した部分は左から順番に計算していきます。
２ ある都市の人口を四捨五入して千の位までの概数で表すと約13000人でした。この都市の人口として考えられるのは何人以上何人以下ですか。
10点
千の位までの概数ということは，3が四捨五入されたあとの数字だということです。四捨五入して千の位が3になる数はどんな範囲の数でしょう。
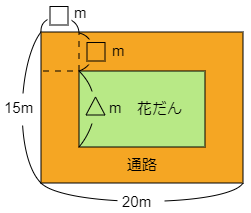
３ たて15m，横20mの土地に花だんを作ります。花だんの周りには，幅が一定の通路を作ります。
次の問いに答えなさい。
10点×3=30(点)
(1) 通路の幅を2mにすると，通路の面積は何m2ですか。
考え方は2通りです。考え方①が簡単ですが，考え方②でもできるようになっておきましょう。
考え方① 通路の面積ではなく，花壇の面積を求めて全体の面積から引けば，通路の面積が求められます。
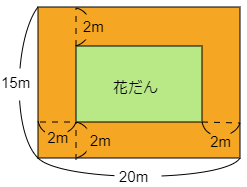
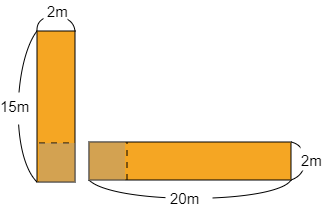
考え方② 次の部分を2つずつ足すと，四隅の部分が2回ずつ足されてしまいます。よってあとからこの部分の正方形4つ分を引きます。
(2) 通路の幅を□m，花だんのたての長さを△mとすると，□と△の関係を式に表しなさい。
答え方は複数あります。そのうちの1つを書くのでOKです。
表し方① □と△で表した式が土地のたての長さ(15m)と等しい，という関係の式
表し方② 土地のたての長さ(15m)から通路2つ分を引くと花だんのたての長さに等しい，という関係の式
などが考えられます。
(3) 花だんのたてと横の長さの合計が23mのとき，通路の幅の長さを求めなさい。
通路がなければ花だんのたてと横の合計は 15+20=35(m) です。通路の幅が1m増えると花だんのたてと横の合計は何m小さくなるでしょうか。それを考えてみましょう。
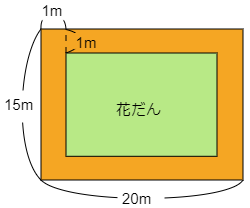通路の幅が1mの場合はこのようになっています。花だんのたてと横の合計は何m小さくなったでしょうか。
４ 1冊130円のノートを4冊と，1個30円のグミを何個か買って1000円を払うとおつりが270円でした。
次の問いに答えなさい。
10点×2=20(点)
(1) グミを何個買いましたか。
まずは支払った合計金額を計算しましょう。そこからノート4冊分の代金を引くと，残った金額がグミを買った代金です。
(2) 残ったおつりで1個20円のガムと1個15円のあめをあわせて15個買って，お金を使い切りました。ガムとあめはそれぞれ何個ずつ買いましたか。
15個全部ガムを買ったとすると 20×15=300 円です。これだと 300−270=30 円オーバーしています。ここから1つだけガムの代わりにあめを買うと，代金が 20−15=5 円減ります。また，ガムを2個減らして代わりにあめを2個買えば，5×2=10 円減らすことができます。30円減らすためにはガムの代わりにあめを何個買えばいいでしょうか。
