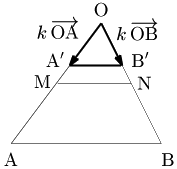平面ベクトルの応用｜三角形の内部と2直線の交点(3通り)をスライドでやさしく解説

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学B　第1章　ベクトル

	スライド	ノート	問題
1. ベクトルと有向線分
2. ベクトルの演算
3. ベクトルの成分
4. ベクトルの内積
5. 位置ベクトル
6. ベクトル方程式
7. 平面ベクトルの応用
8. 空間ベクトル
9. 空間ベクトルの成分
10. 空間ベクトルの内積
11. 空間の位置ベクトル
12. 空間ベクトルの応用
13. 空間のベクトル方程式

7．平面ベクトルの応用

　平行でなく，かつ $\vec{0}$ でない2つのベクトル $\vec{O A}$ と $\vec{O B}$ を用いて $\vec{O P} = s \vec{O A} + t \vec{A B}$ によって定められる点Pは，実数 $s$ と $t$ を適当に定めることで平面上を自由に動くことができる．
　ここで $s$ と $t$ に $s + t = 1$ という制限を加えると，最早点Pは平面上を自由に動き回ることができない．動くことのできる範囲は直線AB上だけである．そして今，更に $s ≧ 0$ かつ $t ≧ 0$ という制限を加えると点Pの動ける範囲はどうなるであろうか．それを以下でみていこう．

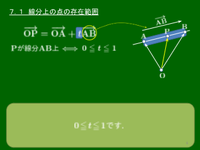
7.1　線分上の点の存在範囲

点が線分上にあるための条件

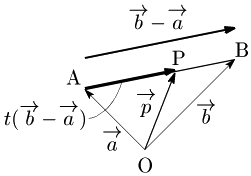
　直線AB上の点Pは $\vec{O P} = \vec{O A} + t \vec{A B}$ と表される．ここで

Pが線分AB上 $⟺ 0 ≦ t ≦ 1$

となることが，下のアニメーションからわかる：

**アニメーション**
$t$ の値が0以上1以下のときのみ
Pは線分AB上にある

　 $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ， $\vec{O P} = \vec{p}$ とおく． $\vec{O P} = \vec{O A} + t \vec{A B}$ を $\vec{a}, \vec{b}, \vec{p}$ で表して

$\vec{p} = \vec{a} + t (\vec{b} - \vec{a}) (0 ≦ t ≦ 1)$

　整理して

$\vec{p} = (1 - t) \vec{a} + t \vec{b} (0 ≦ t ≦ 1)$

　ここで， $1 - t = s (⟺ s + t = 1)$ とおくと，

$\begin{aligned} \vec{p} = s \vec{a} + t \vec{b} ({\underset{―}{s + t = 1, 0 ≦ t ≦ 1}}_{①}) \\ ⟺ & \vec{p} = s \vec{a} + t \vec{b} ({\underset{―}{s + t = 1, s ≧ 0, t ≧ 0}}_{②}) \end{aligned}$

　これが，点Pが線分AB上にある条件である．

※　①と②は全く同じ条件を指しているが，この言い換えはグラフで考えると理解しやすい．詳しくはスライド 参照

点Pが線分AB上にあるための条件　点Pが $\vec{O P} = s \vec{O A} + t \vec{O B}$ で表されるとき，Pが線分AB上にあるための条件は
$s + t = 1, s ≧ 0, t ≧ 0$

　この結果は次節にある，点が三角形の周や内部にある条件で用いられる．

補足

線分の両端を含まない場合

　点Pが線分AB上にあり，かつ線分の両端であるAとBを含まない場合は，上のアニメーションから $0 < t < 1$ となるから

$\vec{O P} = s \vec{O A} + t \vec{O B}, s + t = 1, s > 0, t > 0$

となる．

7.2　三角形の内部を表すベクトル

まずは線分上の点についての例から

　 $\vec{O P} = s \vec{O A} + t \vec{O B}$ ， $s + t = 2$ ， $s ≧ 0$ ， $t ≧ 0$ で表される点Pを考えよう．私たちが先に学習したのは係数の和が1，すなわち $s + t = 1$ の場合であって， $s + t = 2$ の場合についてはまだ知識がない．しかし今， $s + t = 2$ の両辺を2で割って

$\frac{s}{2} + \frac{t}{2} = 1$

というように右辺を1にしてやると， $\frac{s}{2}$ と $\frac{t}{2}$ の和が1で，しかも $s ≧ 0$ ， $t ≧ 0$ から $\frac{s}{2} ≧ 0$ ， $\frac{t}{2} ≧ 0$ である．そこで $\vec{O P} = s \vec{O A} + t \vec{O B}$ の右辺を書き換えて

$\vec{O P} = \frac{s}{2} \cdot 2 \vec{O A} + \frac{t}{2} \cdot 2 \vec{O B}$

という具合に無理に $\frac{s}{2}$ や $\frac{t}{2}$ を作り出し， $2 \vec{O A} = \vec{O C}$ ， $2 \vec{O B} = \vec{O D}$ とおくと

$\vec{O P} = \frac{s}{2} \cdot \vec{O C} + \frac{t}{2} \cdot \vec{O D}$

となる．すると， $\vec{O C}$ と $\vec{O D}$ の係数が共に0以上で，和が１となっているから，前節の結論により点Pは線分 $C D$ 上にあることがわかる．

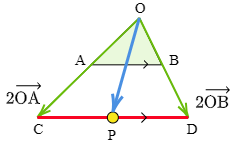
　ここでのポイントは，

係数の和を1にして，前節の結論に帰着させる

ことにある．

次に線分上の点についての一般論

　 $\vec{O P} = s \vec{O A} + t \vec{O B}$ ， $s + t = k$ ， $s ≧ 0$ ， $t ≧ 0$ によって表される点Pを考えよう．

　 $k = 0$ のときは， $s = t = 0$ であるから，このとき $\vec{O P} = \vec{0}$ ，すなわちPはOと重なる．

　 $k \neq 0$ のときは， $s + t = k$ の両辺を $k$ で割ると，

$\frac{s}{k} + \frac{t}{k} = 1$

となるから，

$\vec{O P} = s \vec{O A} + t \vec{O B} = \frac{s}{k} \cdot k \vec{O A} + \frac{t}{k} \cdot k \vec{O B}$

という具合に書き換える．すると $s ≧ 0$ ， $t ≧ 0$ から $\frac{s}{k} ≧ 0$ ， $\frac{t}{k} ≧ 0$ であるから， $k \vec{O A} = \vec{O C}$ ， $k \vec{O B} = \vec{O D}$ となる点 $C, D$ をとると，

$\vec{O P} = \frac{s}{k} \cdot \vec{O C} + \frac{t}{k} \cdot \vec{O D}$

と表され，前節の結論により点Pは線分CD上にあることがわかる．

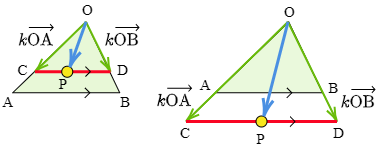
左が $0 ≦ k ≦ 1$ の場合，右が $k ≧ 1$ の場合．いずれもABとCDは平行で，Pが線分CD上のどこにあるかは $s$ と $t$ の値によって決まる．

点が線分上にあるための条件　 $\vec{O P} = s \vec{O A} + t \vec{O B}, s + t = k, s ≧ 0, t ≧ 0$ によって表される点Pは， $k \vec{O A} = \vec{O C}$ ， $k \vec{O B} = \vec{O D}$ となる点 $C, D$ をとると，線分CD上にある．

　先ほど 点Pが線分AB上にあるための条件 を確認したが，それはこの条件式の $k = 1$ の特別な場合に過ぎない．

ではいよいよ点が三角形の周及び内部にあるための条件

例題　△OABに対して，点Pが $\vec{O P} = s \vec{O A} + t \vec{O B}, s + t ≦ 1, s ≧ 0, t ≧ 0$ を満たしながら動くとき，点Pの存在範囲を求めよ．

こたえ

　 $s + t = k$ とおく． $s + t ≦ 1$ ， $s ≧ 0$ ， $t ≧ 0$ より $0 ≦ k ≦ 1$ である．今，この範囲にある $k$ を1つ固定する．(例えば $k = \frac{2}{3}$ というように決めておく．)

　その決めた $k$ の値が0だった場合は， $s = t = 0$ であるから，このとき $\vec{O P} = \vec{0}$ ，すなわちPはOと一致する．

　 $k \neq 0$ のときは，すぐ上で確認したように， $k \vec{O A} = \vec{O C}$ ， $k \vec{O B} = \vec{O D}$ となる点 $C, D$ をとると，点Pは線分CD上にある．

　ここで固定していた $k$ を $0 ≦ k ≦ 1$ の範囲で動かすと，Pは△OABの周及び内部にあることがわかる．

　答え　点Pの存在範囲は，△OABの周及び内部

三角形の周及び内部にある条件　 $\vec{O P} = s \vec{O A} + t \vec{O B}$ で表される点Pについて，Pが△OABの周及び内部にあるための条件は

$s + t ≦ 1, s ≧ 0, t ≧ 0$

補足

点が三角形の内部にあるための条件

　上の補足 で述べたように，点Pが線分AB上にあり，かつ線分の両端であるAとBを含まない場合は，

$\vec{O P} = s \vec{O A} + t \vec{O B}, s + t = 1, s > 0, t > 0$

というように不等号の下の「＝」がなくなる．よって点が三角形の(周を除く)内部に存在するための条件は，三角形の「周及び内部」の場合での条件で，不等号の下の「＝」をすべてなくした次の条件になる：

三角形の内部にあるための条件　 $\vec{O P} = s \vec{O A} + t \vec{O B}$ で表される点Pについて，Pが△OABの内部にあるための条件は

$s + t < 1, s > 0, t > 0$

例題　△OABにおいて， $\vec{O P} = s \vec{O A} + t \vec{O B} (s + t ≦ \frac{1}{2}, s ≧ 0, t ≧ 0)$ を満たす点Pは，どのような図形上にあるか．

答

　解答例を表示する

　 $0 < k ≦ \frac{1}{2}$ なる $k$ を1つ固定し， $s + t = k$ ， $s ≧ 0$ ， $t ≧ 0$ で考える．
　 $s + t = k$ の両辺を $k$ で割ると $\frac{s}{k} + \frac{t}{k} = 1$ となるから， $\vec{O P} = s \vec{O A} + t \vec{O B}$ の右辺を書き換えて，

$\begin{aligned} \vec{O P} & = s \vec{O A} + t \vec{O B} \\ = \frac{s}{k} \cdot k \vec{O A} + \frac{t}{k} \cdot k \vec{O B} \\ = \frac{s}{k} \vec{O A^{'}} + \frac{t}{k} \vec{O B^{'}} \\ (\frac{s}{k} + \frac{t}{k} = 1, \frac{s}{k} ≧ 0, \frac{t}{k} ≧ 0) \end{aligned}$

　ただし，A $^{'}$ ，B $^{'}$ は $\vec{O A^{'}} = k \vec{O A}$ ， $\vec{O B^{'}} = k \vec{O B}$ を満たす点である．
　この結果により，Pは線分 $A^{'} B^{'}$ 上を動くことがわかる．
　ここで，固定していた $k$ を $0 < k ≦ \frac{1}{2}$ で動かし，また $k = 0$ のとき，PはOと一致するから，Pの存在領域は，辺OA，OBの中点をそれぞれM，Nとすると，△OMNの周及び内部である．

7.3　2直線の交点を表すベクトル（3つの解法）

交点のベクトルを求める3つの方法

　次の例題は教科書に必ずといってよいほど登場しているものであるが，その解法については大抵1通りしか掲載されていない．次の「答その1」がそれだ．しかしこの問題には他にもいくつかの解法があり，加えて「答その1」よりも「答その2」が，「答その2」よりも「答その3」が，よりスピーディーに解ける方法となっている．

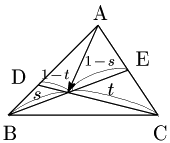
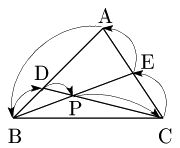
例題　△ABCにおいて，辺ABを $2 : 1$ に内分する点をD，辺ACの中点をEとし，BE，CDの交点をPとするとき， $\vec{A P}$ を $\vec{A B}$ ， $\vec{A C}$ で表せ．

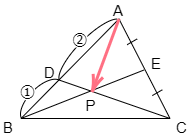
答その1

負担は大きいが共通テストでの誘導はこれ

解法のポイント
　 $\vec{0}$ でなく，平行でない2つのベクトル $\vec{a}, \vec{b}$ について， $\begin{aligned} s \vec{a} + t \vec{b} & = s^{'} \vec{a} + t^{'} \vec{b} \\ ⟺ s = s^{'}, & t = t^{'} \end{aligned}$