高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [無料] | ||
| 2. 一般角の三角関数 | [無料] | ||
| 3. 三角関数の性質 | [無料] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |
演習問題
問題１【発展】
$xy$ 平面上の曲線 $y=x^2$ 上の3点を， $x$ 座標の小さいものから順にA，B，Cとする．AとBの $x$ 座標の差は $a$ ($a$ は正の定数)，BとCとの $x$ 座標の差は1，という関係を保ちながら3点A，B，Cが動く．
∠CABが最大になるときの，点Aの $x$ 座標を $a$ で表せ．また，∠CABが最大になるときに，∠ABCが直角になるような $a$ の値を求めよ．
(東京大)
東京大学(1982)の問題です．東大では他にも放物線上に3点をとって三角形を考えさせる問題(例えば2004年 )があります．難しいですが，学習効果はそれに見合うだけのものはあります．ポイントは
ポイント
直線のなす角は $\tan$ の加法定理で考える
ということです．
解答
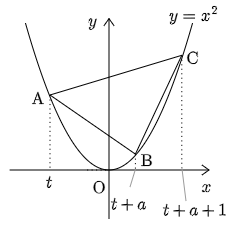
点Aの $x$ 座標を $t$ とすると，点B，Cの $x$ 座標はそれぞれ $t+a$， $t+a+1$ となる．直線AB，ACが $x$ 軸と正の向きとのなす角をそれぞれ $\alpha,\ \beta$ とすると，
\[\tan\alpha=2t+a,\ \tan\beta=2t+a+1\]
である．
補足 放物線 $y=x^2$ 上の任意の異なる2点 $(p,\ p^2)$，$(q,\ q^2)$ を結ぶ直線の傾きは\[\frac{q^2-p^2}{q-p}=p+q\]となります．つまり2点の $x$ 座標の和がその2点を結ぶ直線の傾きとなります．
従って
\[\begin{align*} \tan(\beta-\alpha)&=\frac{\tan\beta-\tan\alpha}{1+\tan\beta\tan\alpha}\\[5pt] &=\frac1{1+(2t+a)(2t+a+1)}\\[5pt] &=\frac1{1+A(A+1)}\\[5pt] &=\frac1{\left(A+\dfrac12\right)^2+\dfrac34} \end{align*}\]
（ただし，$2t+a=A$ とおいた．）
$\left(A+\dfrac12\right)^2+\dfrac34>0$ であるから，$\tan(\beta-\alpha)>0$．従って $\tan(\beta-\alpha)$ が最大となるとき，2直線ABとACのなす角，すなわち∠CABは最大となる．
それは $A+\dfrac12=0$ となるときで，$2t+a+\dfrac12=0$，すなわち $\underline{t=-\dfrac a2-\dfrac14}$ となるときである．
また，直線BCの傾きは $2t+2a+1$ であるから，∠ABCが直角になるとき，2直線ABとBCの傾きの積が $-1$ より
\[(2t+a)(2t+2a+1)=-1\]
\[-\dfrac12\left(a+\dfrac12\right)=-1\]
\[\therefore \underline{a=\dfrac32}\]