高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |

5.1 sin, cos の加法定理
[1] sin(α+β)=sinαcosβ+cosαsinβ[2] sin(α−β)=sinαcosβ−cosαsinβ[3] cos(α+β)=cosαcosβ−sinαsinβ[4] cos(α−β)=cosαcosβ+sinαsinβ
証明
[4]
P(cosα,sinα),Q(cosβ,sinβ) とおく.
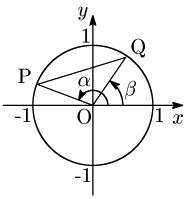
距離の公式により, PQ2=(cosα−cosβ)2+(sinα−sinβ)2=2{1−(cosαcosβ+sinαsinβ)}
ここで,P,Qを原点を中心に −β だけ回転した点をそれぞれP′,Q′ とすると,P′(cos(α−β),sin(α−β)),Q′(1,0) となる:
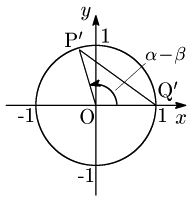
再び距離の公式により, P′Q′2={cos(α−β)−1}2+{sin(α−β)−0}2=2{1−cos(α−β)} PQ2=P′Q′2 により, 2{1−(cosαcosβ+sinαsinβ)}=2{1−cos(α−β)} 整理して cos(α−β)=cosαcosβ+sinαsinβ
[3]
[4] で β を −β におきかえると, cos{α−(−β)}=cosαcos(−β)+sinαsin(−β)∴cos(α+β)=cosαcosβ−sinαsinβ
[1]
[3] で α を α+π2 におきかえると, cos{(α+π2)+β}=cos(α+π2)cosβ−sin(α+π2)sinβ∴−sin(α+β)=−sinαcosβ−cosαsinβ∴sin(α+β)=sinαcosβ+cosαsinβ
[2]
[1] で β を −β におきかえると, sin{α+(−β)}=sinαcos(−β)+cosαsin(−β)∴sin(α−β)=sinαcosβ−cosαsinβ
■
例
sin712π=sin(π3+π4)=sinπ3cosπ4+cosπ3sinπ4=√32⋅1√2+12⋅1√2=√6+√24_
cos712π=cos(π3+π4)=cosπ3cosπ4−sinπ3sinπ4=12⋅1√2−√32⋅1√2=√2+√64_

5.2 tan の加法定理
[1] tan(α+β)=tanα+tanβ1−tanαtanβ[2] tan(α−β)=tanα−tanβ1+tanαtanβ
証明
tan(α+β)=sin(α+β)cos(α+β)=sinαcosβ+cosαcosβcosαcosβ−sinαsinβ=sinαcosβcosαcosβ+cosαsinβcosαcosβ1−sinαsinβcosαcosβ=tanα+tanβ1−tanαtanβ β を −β におきかえると, tan{α+(−β)}=tanα+tan(−β)1−tanαtan(−β)∴tan(α−β)=tanα−tanβ1+tanαtanβ
■

5.3 直線の傾きと tan
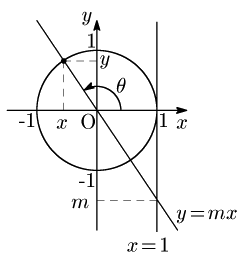
直線 y=mx と x 軸の正の向きとのなす角を θ とすると,tanθ の値は,「2.2 単位円における三角関数」で確認したように2直線 y=mx と x=1 との交点の y 座標として現れる:
tanθ=m
(ただし,0≦θ<π,θ≠π2)
このとき,直線 y=mx に平行である直線 y=mx+n と x 軸の正の向きとのなす角も θ であるから,一般に次が成り立つ:
直線の傾きとtan 直線 y=mx+n と x 軸の正の向きとのなす角を θ とすると, tanθ=m (ただし,0≦θ<π,θ≠π2)

5.4 2直線のなす鋭角
2直線 y=m1x+n1, y=m2x+n2 のなす鋭角を θ とすると,tanθ=|m1−m21+m1m2|
証明
2直線 y=m1x+n1,y=m2x+n2 と x 軸の正の向きとのなす角をそれぞれ θ1,θ2 (ただし,0≦θ<π,θ≠π2) とすると, tanθ1=m1, tanθ2=m2 である.
ここで,θ1−θ2=A とおくと,2直線のなす鋭角 θ,及び tanθ は,A の値によって次の4通りに場合分けされる:
[1] 0≦A<π2 のとき,θ=A ∴tanθ=tanA [2] π2<A<π のとき,θ=π−A ∴tanθ=tan(π−A)=−tanA [3] −π2<A<0 のとき,θ=−A ∴tanθ=tan(−A)=−tanA [4] −π<A<−π2 のとき,θ=π+A ∴tanθ=tan(π+A)=tanA
上のいずれの場合も, tanθ=|tanA| であるから, tanθ=|tanA|=|tan(θ1−θ2)|=|tanθ1−tanθ21+tanθ1tanθ2|=|m1−m21+m1m2|
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |

