高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |

2.1 三角関数の定義
三角関数とは何か
数学Ⅰの三角比のところで,角 θ を 0∘ や 90∘ 以上に拡張した際のアイデアは,そのまま一般角 θ に対する sin,cos,tan に適用することができる.
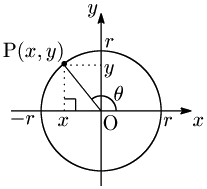
x 軸の正の向きを始線とする一般角 θ の動径と,原点を中心とする半径 r の円との交点をPとし,その座標を (x, y) とする.このとき,sinθ,cosθ,tanθ を次で定義する:
三角関数の定義 sinθ=yrcosθ=xrtanθ=yx (θ≠π2+nπ, nは整数)
この定義によれば,sinθ,cosθ,tanθ の各値は,相似な図形を考えればわかるように半径 r にはよらず,θ によってただ1つ定まる.つまり角 θ の関数である.これら sinθ,cosθ,tanθ を三角関数という.
例 θ=−π3 のときの,sinθ,cosθ,tanθ
答 −π3 の動径と,半径2の円との交点をPとすると,Pの座標は (1,−√3) であるから,
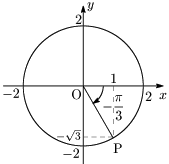
sin(−π3)=−√32=−√32cos(−π3)=12tan(−π3)=−√31=−√3
代表的な三角関数の値をまとめると次の表のようになる:
| θ | 0 | π6 | π4 | π3 | π2 |
| sinθ | 0 | 12 | 1√2 | √32 | 1 |
| cosθ | 1 | √32 | 1√2 | 12 | 0 |
| tanθ | 0 | 1√3 | 1 | √3 | – |
| θ | π2 | 2π3 | 3π4 | 5π6 | π |
| sinθ | 1 | √32 | 1√2 | 12 | 1 |
| cosθ | 0 | −12 | −1√2 | −√32 | 0 |
| tanθ | – | −√3 | −1 | −1√3 | 0 |

2.2 単位円における三角関数
三角関数は単位円で考えるのが基本
原点を中心とする半径1の円を単位円という.
単位円で三角関数を考えると,半径 r=1 であるから次のようになる:
単位円での三角関数 sinθ=ycosθ=xtanθ=yx
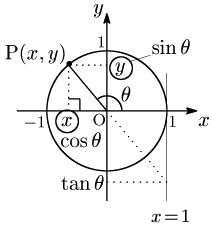
今後三角関数は基本的に単位円を用いて考えていくことになる.その理由は何か.単に sinθ,cosθ が分数の表記を取らないからラクだというのは些細なメリットで,それよりずっと大きなメリットは図のように角 θ の動径をOPとすると,
sinθ はPの y 座標そのもの
cosθ はPの x 座標そのもの
となることである.つまり
三角関数を単位円で考えることの意義
sinθ, cosθ の視覚化
であり,これは誠に重要である.
補足
第2,3象限での tanθ の視覚化
θ が第2,第3象限の角のとき,tanθ の視覚化については次のように考える:
tanθ=yx=−y−x=m1=m
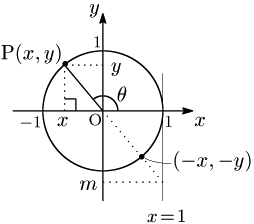
※2点 (x, y), (−x, −y) は原点に関して対称である.
例題 0≦θ<2π のとき,cosθ=−12 を満たす θ の値はを求めよ.
こたえ
解答例を表示する
2.3 三角関数の符号と取りうる値の範囲
三角関数の符号
三角関数の符号も単位円で考える
単位円で考えたときの三角関数は
sinθ=y, cosθ=x, tanθ=yx
であったから,sinθ は y 座標に,cosθ は x 座標にそれぞれ関係している.そして tanθ は yx であったから, sinθ と cosθ の符号を掛けたものとして考えることができる.
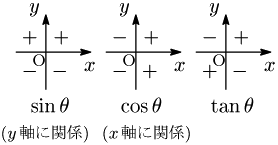
三角関数の取りうる値の範囲
三角関数の値域も単位円で考える
すぐ上の符号のときと同様に,単位円で三角関数を考えてみる.単位円とは原点を中心とする半径1の円のことであったから,x 座標,y 座標とも −1 以上 1 以下の値しかとれない.つまり sinθ や cosθ のとりうる値の範囲は,−1 以上 1 以下である.
一方 tanθ の方は,上の視覚化のところで見たように,いくらでも大きな値や小さな値がとれる.すなわち tanθ のとりうる値の範囲は実数全体である.
三角関数のとりうる値の範囲−1≦sinθ≦1−1≦cosθ≦1
tanθ はすべての実数値をとりうる

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |