高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [会員] | [会員] | |
| 2. 三角比の相互関係 | [会員] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |
演習問題
※以下の問題では,△ABCにおいて下図のように∠A,∠B,∠Cをそれぞれ A,B,C (斜体)で表し,辺BC,CA,ABをそれぞれ a,b,c (小文字の斜体)で表すものとする.
問題1【基本】 ヒント ヒント
次の条件を満たす△ABCは,どのような形の三角形か.sinA=2cosBsinC
問題2【標準】 ヒント ヒント
△ABCにおいて,次の等式を証明せよ.acosAsinC=(b−acosC)sinA
問題3【標準】 ヒント
1辺の長さが2である正四面体OABCにおいて,辺OAの中点をMとする.辺BC上に点Pをとるとき,線分PMの長さの最小値を求めよ.
問題4【発展】
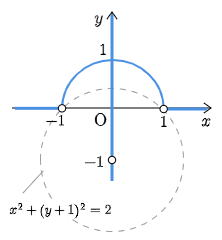
座標平面上の3点 A(1, 0),B(−1, 0),C(0, −1) に対し, ∠APC=∠BPC を満たす点Pの軌跡を求めよ.ただし,P≠A, B, C とする.
(東京大)
解答
POINT
三角比は正弦定理,余弦定理を用いてすべて辺の長さの式にするのが定石です.
△ABCの外接円の半径を R とすると,
正弦定理により sinA=a2R, sinC=c2R
余弦定理により cosB=c2+a2−b22ca
これらを与式に代入して
a2R=2⋅c2+a2−b22ca⋅c2R
両辺を 2aR 倍すると
a2=c2+a2−b2
∴b2−c2=0
(b+c)(b−c)=0
b+c≠0 であるから b−c=0.すなわち b=c.
よって△ABCは b=c の二等辺三角形である.
解答
POINT
(1)と同様に,正弦定理,余弦定理を用いてすべて辺の長さの式にします.
正弦定理により sinA=a2R, sinC=c2R
余弦定理により cosA=b2+c2−a22bc, cosC=a2+b2−c22ab
よって
(左辺)=a⋅b2+c2−a22bc⋅c2R=a(b2+c2−a2)4bR(右辺)=(b−a⋅a2+b2−c22ab)⋅a2R=2b2−(a2+b2−c2)2b⋅12R=a(b2+c2−a2)4bR
従って (左辺)=(右辺) となるから示された.
■
解答
POINT
△ABP(ピンク色)に余弦定理を用いて AP2 を求めたのち,直角三角形APM(黄色)に三平方の定理を用いて PM2 を計算します.
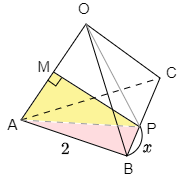
BP=x とおくと,△ABP(ピンク色)において余弦定理により
AP2=22+x2−2⋅2⋅xcos60∘=x2−2x+4
対称性により△PAOは PA=PO の二等辺三角形で,MはAOの中点であるから ∠PMA=90∘.よって△APM(黄色)において三平方の定理により
PM=√AP2−AM2=√(x2−2x+4)−12=√x2−2x+3=√(x−1)2+2
よって x=1 のとき,PMは最小値 √2 をとる.
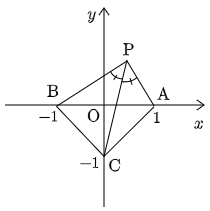
反射的に正弦定理を使いたくなりますが,場合分けが多くて大変な思いをします.場合分けが多くなる理由は,角度に関する等式となってしまうからです.実際,正弦定理により
△APCで ACsin∠APC=PCsin∠PAC
△BPCで BCsin∠BPC=PCsin∠PAC
AC=BC=√2,∠APC=∠BPC ですから PCsin∠PAC=PCsin∠PBC が成り立ち,整理して
sin∠PAC=sin∠PBC
となります.∠PAC,∠PBCは三角形の内角ですから,この等式成り立つとき
∠PAC=∠PBC または ∠PAC+∠PBC=180°
になります.点Pが上のような場所にあれば話は簡単ですが,以下のようにPはどこにでも存在しうるので,場合分けが多くなるという訳です.
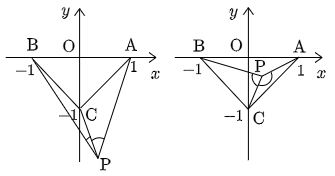
従ってこれまで同様に,角度ではなく辺の長さで考察するのが良さそうです.
解答
1° 点Pが直線AC,またはBC上にあるとき,明らかに ∠APC≠∠BPC
2° 1°でないとき,△APCと△BPCが存在する.AP=a,BP=b,CP=c とおくと,△APCと△BPCにおける余弦定理により
a2+c2−(√2)22ac=b2+c2−(√2)22bc
b(a2+c2−2)=a(b2+c2−2)
ab(a−b)−c2(a−c)+2(a−b)=0
(a−b)(ab−c2+2)=0
よって a=b または ab−c2+2=0
[1] a=b のとき
Pは線分ABの垂直二等分線,即ち y 軸上にある.ただし,C(0,−1) は除く.
[2] ab−c2+2=0 のとき
変形して ab=c2−2
この式のままではこれ以上の情報が得にくいので,ここから座標を用いた方程式に持ち込みます.この決断力には相当な熟練度が求められます.
P(x, y) とおくと,
√(x−1)2+y2√(x+1)2+y2=x2+(y+1)2−2
この関係が成り立つとき,(右辺)≧0が必要で
x2+(y+1)2≧2 …①
この条件の下で,両辺を2乗して
そして,ここからの変形がとても難しいです.上手に計算していかないとたちまち式が爆発し,計算ミスも誘発しやすく収拾がつかなくなるでしょう.以下の記述はシンプルに見えるかもしれませんが,このような適当な式の塊を作りながら展開するためには優れた千里眼が必要で,時間との戦いである受験会場ではほぼ不可能でしょう..
{(x−1)2+y2}{(x+1)2+y2}={x2+(y+1)2−2}2
(A−2x)(A+2x)={A+2(y−1)}2
(ただし,A=x2+y2+1 とおいた.)
展開して A2−4x2=A2+4(y−1)A+4(y−1)2
(y−1)A+(y−1)2+x2=0
(y−1)A+x2+y2+1_A−2y=0
yA−2y=0
y(A−2)=0
A を元に戻して
y(x2+y2−1)=0
よって y=0 または x2+y2=1
条件①に注意して,求める軌跡は図の青色の線のようになる.