高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [無料] | [会員] | |
| 2. 三角比の相互関係 | [無料] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |

2.三角比の相互関係
2.1 三角比の相互関係
sin, cos, tan は相互に関係がある
sinθ=35 というとき,直角三角形の 高さ斜辺 の値が 35 であったということだから,長さの比が (斜辺):(高さ)=5:3 である.今例えば斜辺が5,高さが3とすれば,残りの底辺については三平方の定理から √52−32=4 と計算できる.すると,sinθ 以外の cosθ, tanθ も,cosθ=45,tanθ=34 と計算できてしまう.
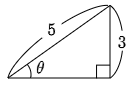
一般に直角三角形の3つの辺から2つを選ぶ方法は3通りあって,これらの各組から三角比が定義されたのであったから,tanθ, sinθ, cosθ のどれか1つでもわかっていれば,あとの2つは計算で求めることができてしまう.何故なら残りの1辺は三平方の定理から求めることができ,従ってその直角三角形の3つの辺の長さの比がすべてわかってしまうからだ.

まずは具体例で相互関係を確認
上の例では sinθ=35 とすれば,それに応じて cosθ, tanθ が決まった.つまり,3つの三角比の間には相互に関係があるのだ.その関係として公式になっているのが3つあるのだが,それをまずは具体例で見ていくとしよう.
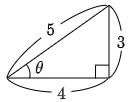
図のように θ をとると,sinθ=35, cosθ=45, tanθ=34 であるから
3=5sinθ (⋯ア), 4=5cosθ (⋯イ), tanθ=34
である.三平方の定理により 32+42=52 が成り立つから,左辺の 3 と 4 を (ア),(イ) に置き換えて
(5sinθ)2+(5cosθ)2=52
52(sinθ)2+52(cosθ)2=52
両辺を 52 で割ると
sin2θ+cos2θ=1
が成り立つ.
※ (sinθ)n はしばしば sinnθ と表される.cosθ や tanθ も同様.
次に, tanθ=34 について,右辺の分母子を (ア),(イ) で置き換えると
tanθ=5sinθ5cosθ
右辺の5を約分して
tanθ=sinθcosθ
最後に先ほど得られた sin2θ+cos2θ=1 の両辺を cos2θ で割ると
sin2θcos2θ+1=1cos2θ∴ (sinθcosθ)2+1=1cos2θ
左辺にすぐ上で得られた tanθ の式を代入して
1+tan2θ=1cos2θ
これら3つの関係式が最重要なものとして今後大活躍することになる.
それではここから相互関係の一般論
上の例と同様にして,一般の場合の三角比の相互関係を導いてみよう.
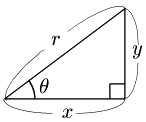
上の図において三平方の定理により x2+y2=r2 が成り立つ.x=rcosθ, y=rsinθ であるから,これらを代入して,
r2cos2θ+r2sin2θ=r2
両辺を r2 で割って,
sin2θ+cos2θ=1 ⋯ ①
次に,
tanθ=yx=rsinθrcosθ=sinθcosθ
となるから,
tanθ=sinθcosθ ⋯ ②
また,①の両辺を cos2θ で割ると,
sin2θcos2θ+1=1cos2θ
(sinθcosθ)2+1=1cos2θ
②を代入して
1+tan2θ=1cos2θ ⋯ ③
①~③は三角比における最重要公式としていつでも直ちに使えるよう記憶しておく必要がある.
三角比の相互関係
[1] sin2θ+cos2θ=1[2] tanθ=sinθcosθ[3] 1+tan2θ=1cos2θ
冒頭で tanθ, sinθ, cosθ には相互に関係があるといったけれども,別の言い方をすれば,tanθ, sinθ, cosθ は同じ θ の値に対してめいめい勝手な値をとることが許されないということである.例えば「sinθ=12 かつ cosθ=13 の場合」などという仮定をおくことはできない.sin2θ+cos2θ=1 とならないからだ.

例題1 θ は鋭角とする.cosθ=34 のとき,sinθ, tanθ の値を求めよ.
こたえ
解答例を表示する
例題2 θ は鋭角とする.tanθ=34 のとき,sinθ, cosθ の値を求めよ.
こたえ
解答例を表示する
2.2 90∘−θ の三角比
θ が鋭角のとき,図より次が成り立つ:
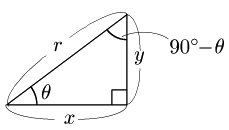
sinθ=yr,sin(90∘−θ)=xrcosθ=xr,cos(90∘−θ)=yrtanθ=yx,tan(90∘−θ)=xy
よって,次のような関係が成り立つことがわかる:
90°-θ の三角比 sin(90∘−θ)=cosθcos(90∘−θ)=sinθtan(90∘−θ)=1tanθ
内容が理解ができたら,次は演習問題 にチャレンジしましょう.

次は,3.三角比の拡張
前は,1.正接,正弦,余弦
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [無料] | [会員] | |
| 2. 三角比の相互関係 | [無料] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |


