スライド ノート 問題
1. 等差数列      
2. 等比数列      
3. Σ(シグマ)と和の公式      
4. 階差数列      
5. 数列の和と一般項      
6. 差をとってできる数列の応用      
7. (等差)×(等比)の和      
8. 群数列      
9. 隣接2項間漸化式(その1)      
10. 隣接2項間漸化式(その2)      
11. 隣接3項間漸化式      

演習問題

問題１【発展】
　2つの関数をf0(x)=x2, f1(x)=x+12 とおく．x0=12 から始め，各 n=1, 2, ⋯ について，それぞれ確率 12 で，xn=f0(xn−1) または xn=f1(xn−1) と定める．
　このとき，xn<23 となる確率 Pn を求めよ．

(京都大)

問題１【発展】

　2つの関数をf0(x)=x2, f1(x)=x+12 とおく．x0=12 から始め，各 n=1, 2, ⋯ について，それぞれ確率 12 で，xn=f0(xn−1) または xn=f1(xn−1) と定める．
　このとき，xn<23 となる確率 Pn を求めよ．

(京都大)

　漸化式の基本的な考え方は

最初か最後で場合分け

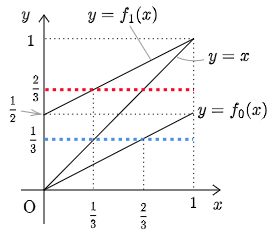
です．この問題では最後で場合分けするのが良いでしょう．本問を考えやすくするポイントは，グラフによる視覚化です．

　xn=f0(xn−1) から xn が決まるときは，確率1で xn<23 となり，xn=f1(xn−1) から xn が決まるときは，xn−1<13 であれば xn<23 となります．となれば，漸化式を作るのにどうしても xn<13 となる確率が欲しくなります．

解答

　P0=1 であり，xn<13 となる確率を Qn とおくと，Q0=0 である．

　上のグラフから，xn<13 であれば，xn+1 は f0(x) から決まろうと f1(x) から決まろうと必ず(すなわち確率1で) xn+1<23 となる．一方，xn≧13 であれば，xn+1 は f0(x) から決まる場合においてのみ xn+1<23 となる．f0(x) と f1(x) のどちらが選ばれるかは確率 12 であるから

Pn+1=Qn⋅1+(1−Qn)⋅12

∴Pn+1=12Qn+12 …①

また，xn+1<13 となるのは，xn<23 かつ f0(x) が選ばれる場合のみであるから

Qn+1=12Pn …②

　①＋② 及び ①－② より

Pn+1+Qn+1=12(Pn+Qn)+12⋯③Pn+1−Qn+1=−12(Pn−Qn)+12⋯④

ここで③において，数列 {Pn+Qn} を1つの数列とみて特性方程式 x=12x+12 を解くと，x=1．

　③を変形して　Pn+1+Qn+1−1=12(Pn+Qn−1)

　よって数列 {Pn+Qn−1} は初項P0+Q0−1=1+0−1=0，項比 12 の等比数列であるから

Pn+Qn−1=0

∴Pn+Qn=1 …⑤

次に④において，数列 {Pn−Qn} を1つの数列とみて特性方程式 x=−12x+12 を解くと，x=13．

　④を変形して　Pn+1−Qn+1−13=12(Pn+Qn−13)

　よって数列 {Pn−Qn−13} は初項P0−Q0−13=1−0−13=23，項比 −12 の等比数列であるから

Pn−Qn−13=23(−12)n

∴Pn−Qn=23(−12)n+13 …⑥

(⑤＋⑥)÷2より

Pn=13(−12)n+23