(数列) Σ(シグマ)と和の公式をスライドでやさしく解説

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学B　第2章　数列

	スライド	ノート	問題
1. 等差数列
2. 等比数列
3. Σ(シグマ)と和の公式
4. 階差数列
5. 数列の和と一般項
6. 差をとってできる数列の応用
7. (等差)×(等比)の和
8. 群数列
9. 隣接2項間漸化式(その1)
10. 隣接2項間漸化式(その2)
11. 隣接3項間漸化式

3. Σ(シグマ)と和の公式

3.1　和の公式

まずは基本となる公式とその証明から

　この節での主な目的は，ギリシャ文字 $Σ$ を用いて数列の和を表すことにあるが，その前に，今後頻繁に使用することになる和の公式を，3つ確認しておく．

和の公式

$[1] 1 + 2 + 3 + \dots + 𝑛 = 12 𝑛 (𝑛 + 1) [2] 12 + 22 + 32 + \dots + 𝑛 2 = 16 𝑛 (𝑛 + 1) (2 𝑛 + 1) [3] 13 + 23 + 33 + \dots + 𝑛 3 = {12 𝑛 (𝑛 + 1)} 2$

　とりわけ[1]と[2]の使用頻度が高く，逆に[3]はほとんど登場しない．

証明

[1]　左辺をよく見れば，初項1，公差1の等差数列の，初項から第 $𝑛$ 項までの和である．等差数列の和の公式は

$𝑆 𝑛 = 12$ ×(項数)×{(初項)＋(末項)}

であったから，

(左辺) $= 12 𝑛 (1 + 𝑛) =$ (右辺)

■

[2]　この証明には，次の恒等式，即ちいかなる値でも成り立つ等式を利用するというのが教科書流である．

　 $(𝑘 + 1) 3 - 𝑘 3 = 3 𝑘 2 + 3 𝑘 + 1$

　この式の両辺に， $𝑘 = 1, 2, 3, \dots$ と代入してみよう．

$23 - 13 = 3 \cdot 12 + 3 \cdot 1 + 1 (𝑘 = 1) 33 - 23 = 3 \cdot 22 + 3 \cdot 2 + 1 (𝑘 = 2) 43 - 33 = 3 \cdot 32 + 3 \cdot 3 + 1 (𝑘 = 3) ⋮ (𝑛 + 1) 3 - 𝑛 3 = 3 𝑛 2 + 3 𝑛 + 1 (𝑘 = 𝑛)$

　これらを辺々加えると，次のようになる：

$(𝑛 + 1) 3 - 13 = 3 (12 + 22 + 32 + \dots + 𝑛 2) + 3 (1 + 2 + 3 + \dots + 𝑛) + 𝑛 \cdot 1$

　右辺の赤色部分に，私たちが今まさに探ろうとしている和 $12 + 22 + 32 + \dots + 𝑛 2$ が出てきた．そこでこの部分を $𝑆$ とおくと，

$(𝑛 + 1) 3 - 1 = 3 𝑆 + 3 \cdot 12 𝑛 (𝑛 + 1) + 𝑛$

　 $3 𝑆$ について解くと，

$3 𝑆 = (𝑛 + 1) 3 - 3 \cdot 12 𝑛 (𝑛 + 1) - (𝑛 + 1)$

　右辺を因数分解して，

$3 𝑆 = 12 (𝑛 + 1) {2 (𝑛 + 1) 2 - 3 𝑛 - 2} = 12 (𝑛 + 1) (2 𝑛 2 + 𝑛) = 12 𝑛 (𝑛 + 1) (2 𝑛 + 1)$

　両辺を3で割って，

$𝑆 = 16 𝑛 (𝑛 + 1) (2 𝑛 + 1)$

■

※別の導出法もいくつか存在している．例えば こちら

[3]　恒等式 $(𝑘 + 1) 4 - 𝑘 4 = 4 𝑘 3 + 6 𝑘 2 + 4 𝑘 + 1$ を用いることで，[2]と同様にして示すことができる．

■

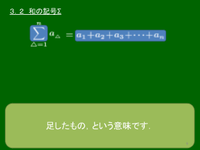
3.2　和の記号Σ

見づらい式を劇的に読みやすくす記号

　例えば，数列 ${𝑎 𝑛}$ について，

$𝑎 1 + 𝑎 2 + 𝑎 3 + 𝑎 4 + 𝑎 5 + 𝑎 6 + 𝑎 7 + 𝑎 8 + 𝑎 9 + 𝑎 10$

というのは

場所を取る，書くのが疲れる，読みにくい

と良いところがない．

　この例がまだ許されるのは，初項から第10項まで隙なく連続しているからであって，もし途中の項，例えば

$𝑎 1 + 𝑎 2 + 𝑎 3 + 𝑎 4 + 𝑎 5 + 𝑎 7 + 𝑎 8 + 𝑎 9 + 𝑎 10$

のように $𝑎 6$ が抜けていたら，そのことに瞬時に気づくことは非常に難しい．

　そこで数学者は便利な記号を発明した． $Σ$ である．

　この記号を用いれば，最初の和は

$10 \sum 𝑘 = 1 𝑎 𝑘$

と表現され，

場所をとらない，書きやすい，読みやすい

という具合に，先程の欠点がすべて解消される．

　一般に， $𝑛 \sum △ = 1 𝑎 △$ は
$𝑎 1 + 𝑎 2 + 𝑎 3 + \dots + 𝑎 𝑛$

を意味する．

和の記号 $Σ$

$𝑛 \sum △ = 1 𝑎 △ = 𝑎 1 + 𝑎 2 + 𝑎 3 + \dots + 𝑎 𝑛$

イメージ

例

　 $4 \sum 𝑘 = 1 𝑎 𝑘 = 𝑎 1 + 𝑎 2 + 𝑎 3 + 𝑎 4$

[動かす文字は， $𝑘$ でなくてもよい]

　 $4 \sum 𝑙 = 1 𝑎 𝑙 = 𝑎 1 + 𝑎 2 + 𝑎 3 + 𝑎 4$

[式は具体的なものでもよい]

　 $3 \sum 𝑚 = 1 (2 𝑚 - 1) = (2 \cdot 1 - 1) + (2 \cdot 2 - 1) + (2 \cdot 3 - 1) = 9$

[スタートは1とは限らない]

　 $5 \sum 𝑝 = 3 2 𝑝 = 23 + 24 + 25 = 8 + 16 + 32 = 56$

　冒頭に挙げた，いくつかの和の公式をはじめ，公式として覚えておくべき $Σ$ を使った式には次のようなものがある．

和の公式

[1]　 $𝑛 \sum 𝑘 = 1 𝑐 = 𝑛 𝑐 (𝑐$ は定数)

[2]　 $𝑛 \sum 𝑘 = 1 𝑘 = 12 𝑛 (𝑛 + 1)$

[3]　 $𝑛 \sum 𝑘 = 1 𝑘 2 = 16 𝑛 (𝑛 + 1) (2 𝑛 + 1)$

[4]　 $𝑛 \sum 𝑘 = 1 𝑘 3 = {12 𝑛 (𝑛 + 1)} 2$

[5]　 $𝑛 \sum 𝑘 = 1 (2 𝑘 - 1) = 𝑛 2$ (奇数 $𝑛$ 個の和)

(数列) Σ(シグマ)と和の公式をスライドでやさしく解説

3. Σ(シグマ)と和の公式

3.1 和の公式

まずは基本となる公式とその証明から

証明

3.2 和の記号Σ

見づらい式を劇的に読みやすくす記号

3.3 Σの性質

3.1　和の公式

3.2　和の記号Σ

3.3　Σの性質