高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |
7. 2次方程式の解の配置
7.1 2次方程式の解の配置
方程式の解の配置は目で考えるのが基本
2次方程式の解について，例えば「2つの解がともに正であるための条件」とか，「一方は正で他方は負であるための条件」といったように，方程式の解の性質について問う問題は，しばしば「方程式の解の配置問題」と呼ばれる．こういった問題を考える上での最良の方策は
解を目で捉える
ことである．
方程式の解を目で捉えるとは一体どういうことか？
2次関数 $y=x^2-4x+3$ を例にとろう．このグラフの $x$ 切片，すなわち $x$ 軸と交わる点の $x$ 座標は何であろうか？
$x$ 軸とは $y$ 座標が0である点の集合である．従って関数の $y$ を0とおくと，$0=x^2-4x+3$ 即ち
\[x^2-4x+3=0\]
を $x$ は満たす．これを解くと
\[(x-1)(x-3)=0\ \ \ \ \therefore x=1,\ 3\]
従って $x$ 切片は1と3であることがわかった．
グラフは次のようである：
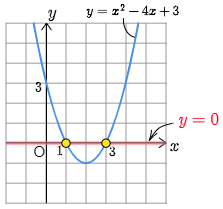
方程式の実数解と $x$ 切片は完全に対応している
私たちが上の操作でやったことは何だったのだろうか？それは2次関数 $y=x^2-4x+3$ のグラフの $x$ 切片を知るのに
2次方程式 $\boldsymbol{x^2-4x+3=0}$ を解いた
のである．そしてこれは逆に考えることもできて，2次方程式 $x^2-4x+3=0$ の実数解が知りたければ
2次関数 $\boldsymbol{y=x^2-4x+3}$ のグラフの $x$ 切片を見ればよい
のである．このように2次方程式の実数解と2次関数のグラフの $x$ 切片は完全に対応しているのであって，従って2次方程式の実数解の配置を考えるには，2次関数のグラフの $x$ 切片がどうなっているかを考えればよいのである．これが
解を目で捉える
の正体である．例えば両方の解が正であるという条件は，グラフが $x$ 軸の正の部分と2点で交わる条件を求めればよい．このような同値な言いかえによって，視覚的に捉えていくことが肝要である．
7.2 いくつかの例
2次方程式の2解について，様々な設定下での条件を考えていこう．
[1] ともに $p$ より大きい
例題 2次方程式 $x^2-2mx-m+2=0$ の重解を含む2つの解が，ともに正であるように，定数 $m$ の値の範囲を定めよ．
考え方
一般に，2次方程式 $ax^2+bx+c=0$ の2つの解が，ともに $p$ より大きいとき，左辺を $f(x)$ とおいた2次関数 $y=f(x)$ のグラフは次のようになっているはずである．
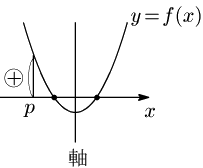
誰もがこのようなグラフを描くためには，次の3条件を課せばよい：
① $D\geqq 0$
② (軸)$>p$
③ $f(p)>0$
補足
上の3条件のどれ1つとして欠けてはならない．実際に次の図からそれを確かめておこう．
①の $D\geqq 0$ だけを満たさない
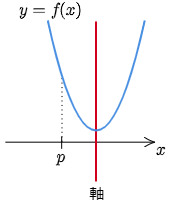
実数解をもたない
②の (軸)$>p$ だけを満たさない
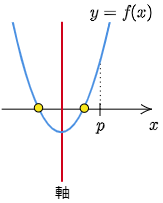
解は共に $p$ 以下
③の $f(p)>0$ だけを満たさない
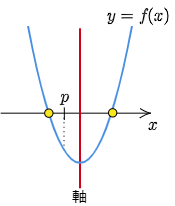
$p$ の両側に解がある
こたえ
2次方程式の左辺を $f(x)$ とおくと，
\[f(x)=(x-m)^2-m^2-m+2\]
と変形できるから，グラフは軸が直線 $x=m$ で，下に凸な放物線である．与えられた2次方程式の判別式を $D$ とすると，2解がともに正，すなわち $x>0$ であるためには次の3つの条件がすべて必要である．
① $D\geqq0$ ② (軸)$>0$ ③ $f(0)>0$
これらの条件はそれぞれ次のようになる
①
\[\begin{align*} D/4=(-m)^2-(-m+2)&\geqq0\\[5pt] m^2+m-2&\geqq0\\[5pt] (m+2)(m-1)&\geqq0\\[5pt] \end{align*}\]
\[\therefore \ \ m\leqq -2,\ 1\leqq m\]
② $m>0$
③ $f(0)=-m+2>0\ \ \therefore m<2$
① かつ ② かつ ③ より，これら3つの条件の共通範囲を求める．
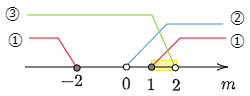
答えは $1\leqq m<2$
[2] ともに $p$ より大きく $q$ 未満
例題 2次方程式 $x^2-4mx-3m+1=0$ が，$0$ と $2$ の間に異なる2つの実数解をもつように，定数 $m$ の値の範囲を定めよ．
考え方
一般に，2次方程式 $ax^2+bx+c=0$ の2つの解が，ともに $p$ より大きく， $q$ より小さいとき，左辺を $f(x)$ とおいた2次関数 $y=f(x)$ のグラフは次のようになっているはずである．
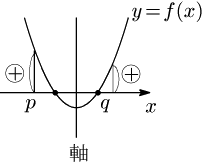
誰もがこのようなグラフを描くためには，次の4条件を課せばよい：
① $D\geqq 0$
② $p<$(軸)$< q$
③ $f(p)>0$
④ $f(q)>0$
こたえ
2次方程式の左辺を $f(x)$ とおくと，
\[f(x)=(x-2m)^2-4m^2+3m+1\]
と変形できるから，グラフは軸が直線 $x=2m$ で，下に凸な放物線である．与えられた2次方程式の判別式を $D$ とすると，異なる2つの解がともに $0$ より大きく，$2$ より小さくなるためには次の4つの条件がすべて必要で，どれ一つとして欠くことができない．
① $D>0$ ② $0<$(軸)$<2$ ③ $f(0)>0$ ④ $f(2)>0$
これらの条件はそれぞれ次のようになる
①
\[\begin{align*} D/4=(-2m)^2-(-3m+1)&>0\\[5pt] 4m^2+3m-1&>0\\[5pt] (m+1)(4m-1)&>0\\[5pt] \end{align*}\]
\[\therefore m<-1,\ \dfrac14<m\]
② $0<2m<2$ $\therefore\ 0<m<1$
③ $-3m+1>0$ $\therefore\ m<\dfrac13$
④ $2^2-4m\cdot2-3m+1>0$ $\therefore\ m<\dfrac5{11}$
① かつ ② かつ ③ かつ ④ より，これら4つの条件の共通範囲を求める．
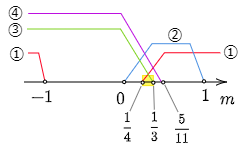
答えは $\dfrac14<m<\dfrac13$
[3] 一方が $p$ より小さく，他方が $p$ より大きい
例題 2次方程式 $2x^2+5mx+m^2-6m-4=0$ が，1より大きい解と，1より小さい解の2つをもつとき，定数 $a$ の値の範囲を定めよ．
考え方
一般に，2次方程式 $ax^2+bx+c=0$ の2つの解の一方が $p$ より小さく，他方が $p$ より大きいとき，左辺を $f(x)$ とおいた2次関数 $y=f(x)$ のグラフは次のようになっているはずである．
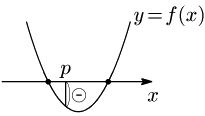
誰もがこのようなグラフを描くためには，次のたった1つの条件を課せばよい：
① $f(p)< 0$
こたえ
2次方程式の左辺を $f(x)$ とおくと，題意の条件は $f(1)<0$ のみである．
\[\begin{align*} f(1)=2\cdot1^2+5m\cdot1+m^2-6m-4<0\\[5pt] m^2-m-2<0\\[5pt] (m+1)(m-2)<0\\[5pt] \end{align*}\]
答えは $-1<m<2$
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |