高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [会員] | [会員] | |
| 3. 2次関数の最大・最小 | [会員] | [会員] | |
| 4. 2次関数の決定 | [会員] | [会員] | |
| 5. 2次関数のグラフと方程式 | [会員] | [会員] | |
| 6. 2次不等式とグラフ | [会員] | [会員] | |
| 7. 2次方程式の解の配置 | [会員] | [会員] |

演習問題
問題2はすべて微妙に異なっているので,数字や不等号の向き,不等号の下の等号の有無に気を付けてください.
問題1【基本】
次の2次不等式を解け.
(1) $(x-1)(x-3)<0$
(2) $x^2-2x+2<2x-1$
(3) $-x^2+4x-3<0$
問題2【基本】
次の2次不等式を解け.
(1) $x^2-4x+5>0$
(2) $x^2-4x+4>0$
(3) $x^2-4x+4\geqq0$
(4) $x^2-4x+4\leqq0$
(5) $x^2-4x+4<0$
問題3【標準】
$a$ を定数とするとき,次の2次不等式を解け.\[x^2-(a+2)+2a<0\]
問題4【標準】
$a$ を定数とするとき,次の不等式を解け.\[ax^2-2ax\leqq0\]
問題5【標準】
2次不等式 $ax^2+bx-3\leqq0$ の解が $x\leqq1,\ 3\leqq x$ となるように定数 $a,\ b$ の値を定めよ.
問題6【標準】
$x$ の方程式 $mx^2+(m-3)x+1=0$ の実数解の個数を求めよ.
問題7【標準】
(1) すべての実数 $x$ に対して,2次不等式 $x^2+2(k-2)x+1\geqq0$ が成り立つような定数 $k$ の値の範囲を求めよ.
(2) ある実数 $x$ に対して,2次不等式 $x^2+2(k-2)x+1<0$ が成り立つような定数 $k$ の値の範囲を求めよ.
問題8【標準】
$1\leqq x\leqq 4$ であるすべての $x$ に対して,不等式 $x^2-2mx+4m+1>0$ が成り立つような定数 $m$ の値の範囲を求めよ.
問題9【標準】
次の不等式を解け
\[4x-3<x^2\leqq 2x\]
問題10【発展】
実数 $x,y$ が $x^2+y^2=4$ を満たすとき.$2x+y^2$ の最大値と最小値を求めよ.
問題11【発展】
実数 $x,y$ が $x^2+y^2=4$ を満たすとき.$2x+y$ の最大値と最小値を求めよ.

2次不等式を考える上で最も有用な思考は,
2次関数のグラフを考える
です.例えば(1)の場合,左辺の $(x-1)(x-3)$ を $y$ とおくと\[y<0\]と表されます.2次関数 $y=(x-1)(x-3)$ のグラフは次のようになります.
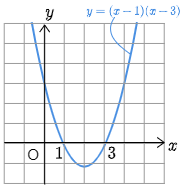
$x$ を動かしたとき, $y$ の値はどうなるでしょうか?
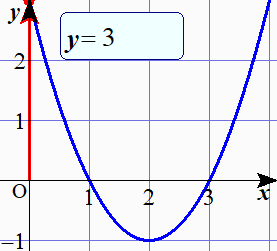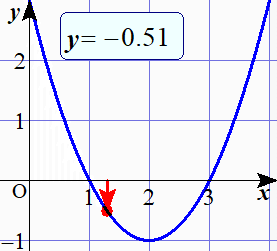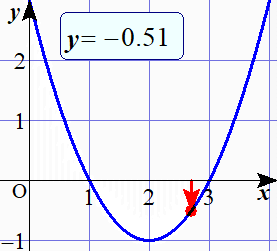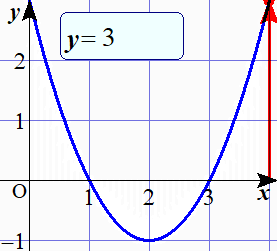
このアニメーションからわかるように, $y<0$ というのはグラフが $x$ 軸より下側にきている場合であって,そのようになっている $x$ の値の範囲はどうなっているのかということが問われている訳です.
解答
(1) $y=(x-1)(x-3)$ とおくと,この2次関数のグラフは図のようになります.

グラフから $y<0$ となる $x$ の値の範囲は\[1<x<3\]
(2) $x^2-2x+2<2x-1$ を整理すると\[x^2-4x+3<0\] これは左辺を因数分解すれば(1)の2次不等式と同じになりますから,答えも当然同じです.
答えは $1<x<3$
(3) 両辺に $-1$ を掛けると\[x^2-4x+3>0\] 故に左辺を $y$ とおいた2次関数は(1)のものと同じになります.(3)では $y>0$ となる範囲ですから,グラフが $x$ 軸よりも上側となっている $x$ の値の範囲を求めればよい訳です.
答えは $x<1,\ 3<x$
重要なアドバイス
(3)のように $x^2$ の係数が負の数であるときには,両辺に $-1$ を掛けて正の数にしてから考えます.グラフを常に下に凸にしておくことで,うっかりミスを減らすことができます.必ず実施するようにしましょう.
ここでも2次関数のグラフが有効です.
解答
(1) 与式の左辺を $y$ とおいて,平方完成すると
\[\begin{align*}
y&=x^2-4x+5\\[5pt]
&=(x-2)^2-2^2+5\\[5pt]
&=(x-2)^2+1\\[5pt]
\end{align*}\]
よってグラフは図のようになります.
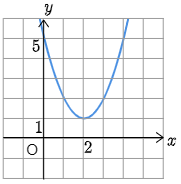
グラフからすべての $x$ で $y>0$ となっています.
答えは すべての実数
補足 グラフに頼らず,平方完成された式で考えることもできます.
$y=(x-2)^2+1$ において,$(x-2)^2$ の部分はどんな $x$ の値に対しても0以上の値となり,更にそれに1を加えるので,常に $y>0$ となります.
(2)~(5) は,左辺がすべて同じ2次関数です.この左辺を $y$ とおいて平方完成すると
\[y=x^2-4x+4=(x-2)^2-2^2+4=(x-2)^2\]
よって $y=x^2-4x+4$ のグラフは図のようになります.
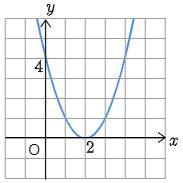
(2) $y>0$ となるのは,グラフから $x=2$ 以外ならどこでもOKです.
答えは $x<2,\ 2<x$
補足 答えは簡単に「$x\neq2$」とだけ書いてもよいでしょう.
(3) $y\geqq0$ となるのは,グラフからすべての実数です.
答えは すべての実数
(4) $y\leqq0$ となるのは,グラフから $x=2$ だけです.$x=2$ 以外はすべて $y>0$ となっています.もちろん $y<0$ となることもありません.
答えは $x=2$
補足 不等式を解くと,大抵の場合答えも ‘<’ や’ >’ の不等号を使った不等式となりますが,この問題のように不等式を解いた結果,等式になるということもあるのです.
(5) グラフからわかるように,$y<0$ となるような $x$ は存在しません.
答えは 解はない となります.
文字式が含まれていて一見難しそうですが,因数分解ができることに気が付けば,それほどでもありません.
与式は\[(x-a)(x-2)<0\]と因数分解できます.この式の左辺を $y$ とおいて2次関数 $y=(x-a)(x-2)$ を考えると,グラフは下に凸で,$x$ 軸と $x=a$ と2で交わります.問題は $y\leqq0$ となる $x$ の値の範囲を求めればよいのでグラフを手掛かりに考えていきましょう.
ところでここで困ったことが起こります.$a$ と2ではどちらが大きいのでしょうか?これがわからないとグラフを描くことができません.問題文を見ても,$a$ と2の大小関係はわかりません.
そんなときは場合分けを行うのです.$a$ と2の大小関係は次の3通りが考えられます.
1° $a<2$ 2° $a=2$ 3° $a>2$
それぞれの場合を丁寧に調べていきます.
解答
与式の左辺を $y$ とおくと\[x^2-(a+2)+2a=(x-a)(x-2)\]と表せます.
1° $a<2$ のとき
グラフは図のようになります.
