高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |
6. 2次不等式とグラフ
6.1 2次不等式
まずは1次不等式の復習から
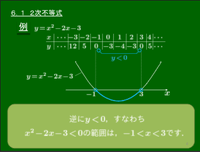
例 1次不等式 $2x-6>0$ を解け．
変形して $2x>6$．$x$ の係数2が正の数であることに注意をして，両辺を2で割ると $x>3$．答えは $x>3$ である．これを視覚的に捉えてみよう．$y=2x-6$ のグラフは次のようになる．
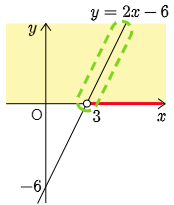
不等式 $2x-6>0$ を解くということは，この関数の値が $y>0$ となる $x$ の値の範囲を考えることに他ならない．これはグラフが黄色で塗られた領域に属する $x$ の値の範囲を考えることで，$x>3$ となることがわかる．
このように不等式というのは
グラフを描いて視覚的に捉える
ことが大切である．
2次不等式は2次関数のグラフから考えるのが基本
例題 次の2次不等式を解け．
(1) $x^2-2x-3>0$
(2) $x^2-2x-3<0$
こたえ
左辺の式はいずれも $x^2-2x-3$ である．この式を変形すると $x^2-2x-3=(x+1)(x-3)$ となるから，グラフは $x$ 軸と $-1$ と $3$ で交わる．従って $y=x^2-2x-3$ のグラフは次のようになる．グラフの上にある表は，$x$ が整数であるいくつかの値と，そのときの $y$ の値である．
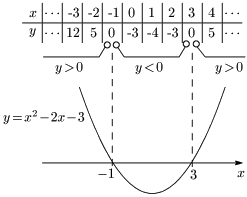
(1) $x^2-2x-3>0$ すなわち $y>0$ のとき，$x<-1,\ 3<x$
(2) $x^2-2x-3<0$ すなわち $y<0$ のとき，$-1<x<3$
一般に次が成り立つ：
$a\!>\!0$ とする．2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が異なる2つの実数解 $\alpha,\beta\ (\alpha<\beta)$ をもつとき，
$ax^2\!+\!bx\!+\!c\!>\!0$ の解は $x\!<\!\alpha,\ \beta\!<\!x$
$ax^2\!+\!bx\!+\!c\!\geqq\!0$ の解は $x\!\leqq\!\alpha,\ \beta\!\leqq\! x$
$ax^2\!+\!bx\!+\!c\!<\!0$ の解は $\alpha\!<\!x\!<\!\beta$
$ax^2\!+\!bx\!+\!c\!\leqq\!0$ の解は $\alpha\!\leqq\!x\!\leqq\!\beta$
補足
$a <0$ のときは，両辺に $-1$ を掛けて，$x^2$ の係数を正にしてから考えるとよい．これはつまらないケアレスミスを防ぐためである．
(このとき不等号の向きが変わるので注意．)
6.2 放物線が $x$ 軸に接する場合
グラフを使って目で考えるのが基本
例題 次の2次不等式を解け．
(1) $x^2-2x+1>0$
(2) $x^2-2x+1\geqq 0$
(3) $x^2-2x+1<0$
(4) $x^2-2x+1\leqq0$
こたえ
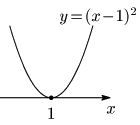
左辺はどれも同じで $x^2-2x+1$．これを0とおいた2次方程式 $x^2-2x+1=0$ は $(x-1)^2=0$ と変形できるから，$x=1$ を重解にもつ．また左辺を $y$ とおいた2次関数 $y=x^2-2x+1$ のグラフは，頂点が $(1,\ 0)$ であるから $x$ 軸に $x=1$ で接する下に凸な放物線である．
よって答えは
(1) $x^2-2x+1>0$ の解は，$x<1,\ 1<x$
(2) $x^2-2x+1\geqq0$ の解は，すべての実数
(3) $x^2-2x+1<0$ の解は，なし
(4) $x^2-2x+1\leqq0$ の解は，$x=1$ (等式！)
※4番目の例では不等式の解が等式となっていることに注意．
$a\!>\!0$ とする．2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が $p$ を重解にもつとき，
$ax^2\!+\!bx\!+\!c\!>\!0$ の解は $x\!<\!p,\ p\ \!<\!x$
$ax^2\!+\!bx\!+\!c\!\geqq\!0$ の解は すべての実数
$ax^2\!+\!bx\!+\!c\!<\!0$ の解は なし
$ax^2\!+\!bx\!+\!c\!\leqq\!0$ の解は $x=p$
6.3 放物線が $x$ 軸と共有点をもたない場合
ここでもグラフを使って目で考えるのが基本
例題 次の2次不等式を解け．
(1) $x^2-2x+2>0$
(2) $x^2-2x+2\geqq 0$
(3) $x^2-2x+2<0$
(4) $x^2-2x+2\leqq0$
こたえ
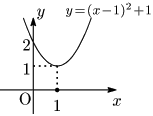
左辺はどれも同じで $x^2-2x+2$．この左辺を $y$ とおいた2次関数 $y=x^2-2x+2$ を考えると， $y\!=\!x^2\!-\!2x\!+\!2\!=\!(x\!-\!1)^2\!+\!1$ となるから，グラフの頂点は $(1,\ 1)$．従ってグラフは $x$ 軸より上側にある下に凸な放物線である．よって
(1) $x^2-2x+2>0$ の解は，すべての実数
(2) $x^2-2x+2\geqq0$ の解は，すべての実数
(3) $x^2-2x+2<0$ の解は，なし
(4) $x^2-2x+2\leqq0$ の解は，なし
$a\!>\!0$ とする．2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ が 実数解をもたないとき，
$ax^2\!+\!bx\!+\!c\!>\!0$ の解は すべての実数
$ax^2\!+\!bx\!+\!c\!\geqq\!0$ の解は すべての実数
$ax^2\!+\!bx\!+\!c\!<\!0$ の解は なし
$ax^2\!+\!bx\!+\!c\!\leqq\!0$ の解は なし
非常によくある間違い
数学Ⅱで複素数を習ったあとにしばしばみられる誤答
問題 $x^2-2x+2<0$ を解け．
誤答 $x^2-2x+2=0$ を解くと，解の公式から $x=1\pm i$．よって
$1-i<x<1+i\ \ \cdots$ (答)
そもそも虚数に大小の概念はない．($2i<3i$ などは正しくない．) 2次不等式を考える際には常に2次関数のグラフとリンクさせて考えると間違いが少ない．
次は，7．2次方程式の解の配置
前は，5．2次関数のグラフと方程式
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |