2次関数と2次方程式は密接に関係しています.
2次関数において,となるの値を考えることは,2次方程式を考えることと同じです.
また,2次方程式を考えることは,2次関数において,となるの値を考えることと同じです.
これは2次関数のグラフにまつわる共有点問題を2次方程式の理論に持ち込んだり,逆に2次方程式の解に関する問題を2次関数のグラフに持ち込んで視覚的に考察したりできるということです.
状況に応じて,こういった2次関数と2次方程式の相互の行き来がスムーズにできるようになることが重要です.
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |

5.2次関数のグラフと方程式
| 5.1 2次関数と2次方程式 | スライド① |
| 5.2 2次関数のグラフと直線 | スライド② |
スライドはぜひ全画面表示で
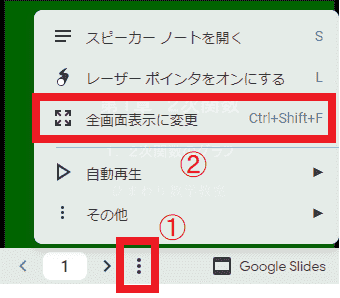
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
スライド① 2次関数と2次方程式
スライド② 2次関数のグラフと直線
次のスライドは,6.2次不等式とグラフ
前のスライドは,4.2次関数の決定

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |
