4. 2次関数の決定(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]		[会員]
2. 関数のグラフの移動	[無料]		[会員]
3. 2次関数の最大・最小	[無料]		[会員]
4. 2次関数の決定	[無料]		[会員]
5. 2次関数のグラフと方程式	[無料]		[会員]
6. 2次不等式とグラフ	[無料]		[会員]
7. 2次方程式の解の配置	[無料]		[会員]

4.　2次関数の決定

4.1　2次関数の決定

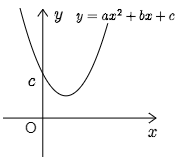
　ここでは与えられた条件を満たす2次関数を決定する方法を学ぶ．

　2次関数は，どんなものでも $y=ax^2+bx+c$ と表すことができるから，まずはこのようにおいてみるとしよう．ここで未知なる文字は $a,\ b,\ c$ の3つである．従って条件が3つ与えられれば原理的には $a,\ b,\ c$ が決定できるはずだ．

　基本姿勢はこれでよいのであるが，条件によってはスタートの式を $y=ax^2+bx+c$ にするより別の式にした方が，ずっと効率的に決定できる場合がある．その最たる例が

頂点や軸の情報がわかっている

場合である．そのときは $y=ax^2+bx+c$ とおかずに，最初から $y=a(x-p)^2+q$ とおけば，$p$ や $q$ が直ちに決定できる．この結果 $y=ax^2+bx+c$ を平方完成するという最も手間がかかる作業が省ける．しかしながら $y=a(x-p)^2+q$ からスタートさせたからといって，要求されている情報数を減らすことに成功した訳ではない．$y=ax^2+bx+c$ のときには $ a,\ b,\ c$ の3つが必要であったが，$y=a(x-p)^2+q$ のときには $a,\ p,\ q$ が必要で，やはり決めなければならない文字は3つあって，最初の場合と変わりはない．

2次関数を決定するときの3つの基本形

　2次関数を決定するには，与えられた条件により次のようにおく：

① 頂点や軸がわかっているとき

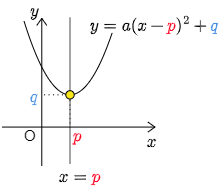
　このケースは比較的簡単に2次関数が決定できる場合で，スタートの式を

\[y=a(x-p)^2+q\]

とおくことがポイントとなる．

例題1　次の条件を満たす2次関数を求めよ．
　グラフの頂点の座標は $(1,2)$で，点 $(2,4)$ を通る．

答

　解答例を表示する

　頂点の座標が $(1,2)$ より，求める2次関数は \[y=a(x-1)^2+2\] とおける．このグラフが点 $(2,4)$ を通るとき， \[4=a(2-1)^2+2\ \ \ \ \therefore a=2\] 　よって， \[\underline{\boldsymbol{y=2(x-1)^2+2}}\ \ \ (y=2x^2-4x+4)\]

② 頂点や軸がわかっていないとき

　この場合が最も面倒で，3文字の連立方程式を解くというのが基本解法である．しかし条件によっては計算の負担を上手く軽減させることができる場合がある．演習問題 のページにある問題4のような場合がそれである．

例題2　次の条件を満たす2次関数はを求めよ．
　グラフが3点 $(1,-2),\ (-2,-5),\ (3,10)$ を通る．

答

　解答例を表示する

　求める2次関数を $y=ax^2+bx+c$ とおくと，条件より \[\left\{\begin{array}{ll} \ a+\ b+\ c=-2&\cdots\mbox{①}\\[5pt] 4a-2b+c=-5&\cdots\mbox{②}\\[5pt] 9a+3b+c=10&\cdots\mbox{③}\\[5pt] \end{array}\right.\] 　②$-$①より，$3a-3b=-3\ \therefore\ a-b=-1\ \cdots$④
　③$-$①より，$8a+2b=12\ \therefore\ 4a+b=6\ \cdots$⑤
　④$+$⑤より，$5a=5\ \therefore\ a=1$
　従って，④より $b=2$，①より $c=-5$
　以上により，$\underline{\boldsymbol{y=x^2+2x-5}}$

③ $x$ 切片がわかっているとき

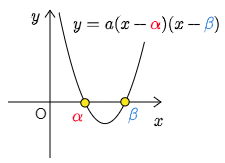
　この条件が最初に与えられるということは，数学Ⅰの分野ではあまりないかもしれない．むしろ $y=ax^2+bx+c$ を変形して $y=a(x-\alpha)(x-\beta)$ とし，$x$ 切片を求めるという方が多かろう．例えば放物線 $y=x^2-3x+2$ の $x$ 切片は $y=(x-1)(x-2)$ と変形して1と2である等々．こういったことが頻繁に必要になるのは，数学Ⅱで学ぶ積分などの分野である．

　まず念のため $y=a(x-\alpha)(x-\beta)$ が2次関数であることを確認しておこう．

\[\begin{align*} y&=a(x-\alpha)(x-\beta)\\[5pt] &=a\{x^2-(\alpha+\beta)x+\alpha\beta\}\\[5pt] &=ax^2\underline{-a(\alpha+\beta)}\,x+\underline{a\alpha\beta} \end{align*}\]

　2つの下線部分 $-a(\alpha+\beta)$ と $a\alpha\beta$ は定数であるから，これは $y=ax^2+bx+c$ の形をしている．従って2次関数であることがわかる．

　次に，このグラフの $x$ 切片が $\alpha$ と $\beta$ であることを確認しておこう．$y=a(x-\alpha)(x-\beta)$ に $x=\alpha$ を代入すると

\[y=a(\alpha-\alpha)(\alpha-\beta)=0\]

となるから 点 $(\alpha,\ 0)$ を通る．従ってグラフの $x$ 切片の1つは $\alpha$ である．同様にして $x=\beta$ を代入しても $y=0$ となるから，グラフのもう1つの $x$ 切片は $\beta$ である．

例題3　次の条件を満たす2次関数を求めよ．
　グラフの $x$ 切片が $-1$ と $2$ であり，点 $(3,4)$ を通る．

答

　解答例を表示する

　$x$ 切片が $-1$ と $2$ であるから，求める2次関数は， \[y=a(x+1)(x-2)\] とおける．このグラフが点 $(3,4)$ を通るから， \[\begin{align*} 4&=a(3+1)(3-2)\\[5pt] \therefore a&=1 \end{align*}\] 　よって， \[y=(x+1)(x-2)\] \[\therefore \underline{\boldsymbol{y=x^2-x-2}}\]

このあとは演習問題 で理解を確認！

次は，5．2次関数のグラフと方程式
前は，3．2次関数の最大・最小

---

高校数学[総目次]

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]		[会員]
2. 関数のグラフの移動	[無料]		[会員]
3. 2次関数の最大・最小	[無料]		[会員]
4. 2次関数の決定	[無料]		[会員]
5. 2次関数のグラフと方程式	[無料]		[会員]
6. 2次不等式とグラフ	[無料]		[会員]
7. 2次方程式の解の配置	[無料]		[会員]