高校数学[総目次]
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [無料] | [会員] | |
| 3. 2次関数の最大・最小 | [無料] | [会員] | |
| 4. 2次関数の決定 | [無料] | [会員] | |
| 5. 2次関数のグラフと方程式 | [無料] | [会員] | |
| 6. 2次不等式とグラフ | [無料] | [会員] | |
| 7. 2次方程式の解の配置 | [無料] | [会員] |

演習問題
基礎から応用・発展まで幅広く問題を取り揃えました.最後の問題12だけは考えにくい難問で,東大に合格するような人の中でも解けるのは3人に1人もいないのではないでしょうか.
問題1【基本】
次の2次関数に最大値,最小値があればそれを求めよ.最大値または最小値をとるときの x の値もあわせて求めよ.
(1) y=x2−4x+5 (2) y=−2x2+4x
問題2【基本】
次の2次関数に最大値,最小値があればそれを求めよ.最大値または最小値をとるときの x の値もあわせて求めよ.
(1) y=x2−4x+5 (0≦x≦1)
(2) y=−2x2+4x (−1<x≦2)
問題3【標準】
a は正の定数とする.0≦x≦a における関数 f(x)=x2−2x について,次の問いに答えよ.
(1) 最小値及び最小値をとるときの x の値を求めよ.
(2) 最大値及び最大値をとるときの x の値を求めよ.
問題4【標準】
a は定数とする.0≦x≦2 における関数 f(x)=x2−2ax について,次の問いに答えよ.
(1) 最小値及び最小値をとるときの x の値を求めよ.
(2) 最大値及び最大値をとるときの x の値を求めよ.
問題5【標準】
a は定数とする.a≦x≦a+2 における関数 f(x)=x2−2x について,次の問いに答えよ.
(1) 最小値及び最小値をとるときの x の値を求めよ.
(2) 最大値及び最大値をとるときの x の値を求めよ.
問題6【標準】
k は定数とする.x の2次関数 y=x2−4kx+3k2+4k+7 の最小値を m とする.
(1) m を k の式で表せ.
(2) m の最大値と,最大をとるときの k の値を求めよ.
問題7【標準】
関数 f(x)=x2−2kx+k2+2k (0≦x≦2) の最小値が3となるような定数 k の値を求めよ.
問題8【標準】
関数 f(x)=ax2−2ax+b (0≦x≦2) の最大値が7,最小値が2となるとき,定数 a, b の値を求めよ.
問題9【発展】
x≧0, y≧0, x+y=2 のとき,xy の最大値と最小値を求めよ.また,最大値・最小値をとるときの x, y の値もあわせて求めよ.
問題10【発展】
x, y の関数 P=x2−2xy+2y2−2x−2y+6 の最小値を求めよ.また,最小値をとるときの x, y の値もあわせて求めよ.
問題11【発展】
(1) 関数 y=x2−2x (0≦x≦3) の最大値,最小値を求めよ.
(2) 関数 (x2−2x)2−2(x2−2x)+5 (0≦x≦3) の最大値と最小値を求めよ.
問題12【難】
関数 f(x)=|x2+ax+b| (−1≦x≦1) の最大値は 12 以上であることを示せ.

2次関数の最大・最小問題を解くときにはいつでもグラフをイメージしながらが考えることが大切です.まずは
下に凸か,上に凸か
です.これがわかったら
軸に関して対称
であることを常に意識しながら考えていきます.
解答
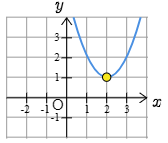
(1) y=x2−4x+5 の2次の係数は1で正の数ですから,グラフは下に凸です.平方完成するとy=(x−2)2+1 従って
最大値は ない
最小値は x=2 で1
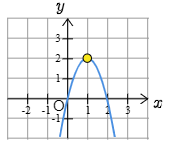
(2) y=−2x2+4x の2次の係数は −2 で負の数ですから,グラフは上に凸です.平方完成するとy=−2(x−1)2+2 従って
最大値は x=1 で2
最小値は ない
問題となっている関数は問題1と同じです.問題1では定義域が実数全体の場合で,2次の係数が正だと最小値は存在しますが,最大値の方はいくらでも大きくなるため存在しませんでした.問題2では定義域に制限があり,この場合ですと最大値と最小値を共に持つ可能性があります.ここでもグラフをイメージすることが欠かせません.まずは
軸が定義域に含まれるかどうか
です.
①YES → 軸のところで最大or最小
②NO → 定義域の両端のところで最大と最小
更に①では定義域の両端での値の大小を判定しますが,その際の視点は
どちらがより軸から遠いか
です.
(2)では区間の片方の端である −1 が定義域に含まれていないことに注意しましょう.
解答
(1)
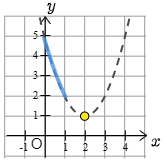
問題1より y=x2−4x+5=(x−2)2+1.従ってグラフの軸は直線 x=2 です.これは定義域 0≦x≦1 に含まれませんから,定義域の両端である 0 と 1 のところで最大値と最小値をとります.グラフが下に凸ですから,軸から最も遠い 0 のところで最大となり,軸に最も近い x=1 で最小となります.答えは
x=0 で最大値5
x=1 で最小値2
となります.
(2)
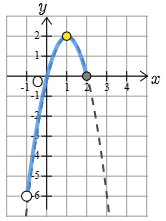
問題1より y=−2x2+4x=−2(x−1)2+2.従ってグラフの軸は直線 x=1 です.これは定義域 −1<x≦2 に含まれますから,グラフが上に凸であることに注意すると,軸のところで最大となります.一方最小の方は,定義域の両端である −1 と2が候補になり,軸からより遠いのは −1 の方です.従って x の値が軸から −1 に近付くにつれどんどん値が小さくなっていきますが,肝心の −1 そのものは定義域に含まれていません!従って答えは
x=1 で最大値2
最小値は ない
となります.
定義域の左端は0に固定されています.右端の a が大きくなるについて,定義域の幅が広がっていきます.2次関数のグラフ方は座標平面上に固定されています.考え方はこれまでと同じで
①下に凸か,上に凸か
②軸は定義域に含まれているか
③軸からより遠い(近い)のはどこか
をグラフとともにイメージすることです.
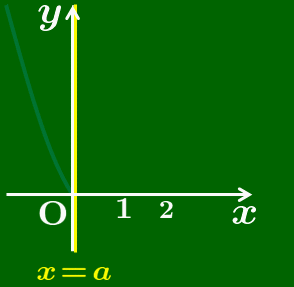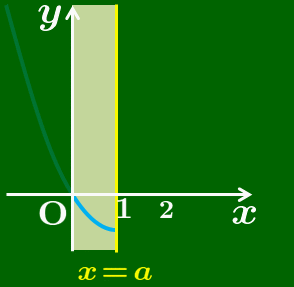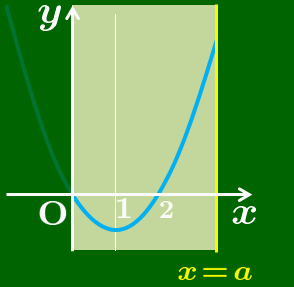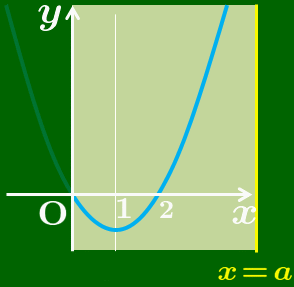
青色のグラフが見えている範囲だけで
最大値と最小値を考える
