高校数学[総目次]

数学Ⅰ　第1章　2次関数

  スライド ノート 問題
1. 2次関数のグラフ [無料]   [会員]
2. 関数のグラフの移動 [無料]   [会員]
3. 2次関数の最大・最小 [無料]   [会員]
4. 2次関数の決定 [無料]   [会員]
5. 2次関数のグラフと方程式 [無料]   [会員]
6. 2次不等式とグラフ [無料]   [会員]
7. 2次方程式の解の配置 [無料]   [会員]

演習問題

問題１【基本】
　次の2次関数のグラフは，2次関数 y=2x2 のグラフをどのように移動したものか．また軸と頂点を求め，グラフをかけ．
(1) y=2x2−1　(2) y=2(x+3)2　(3) y=2(x+3)2−1　

問題２【基本】
　次の2次関数のグラフの軸と頂点を求め，グラフをかけ．
(1) y=2x2−4x+4　(2) y=−x2+2x　(3) y=12x2+2x+3

問題３【標準】
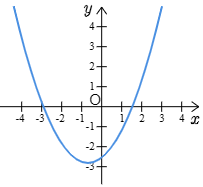
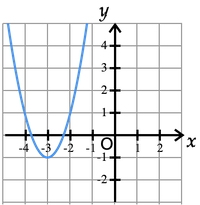
　2次関数 y=ax2+bx+c のグラフが図のようになるとき，次の値の符号を調べよ．
(1) a　(2) b　(3) c
(4) b2−4ac　(5) a+b+c
(6) a−b+c　(7) 4a+2b+c

問題４【標準】
　x の2次関数 y=x2+2k−4 のグラフについて，軸の方程式と頂点の座標を求めよ．また次の各場合についてグラフをかけ．
(1) k<2　(2) k=2　(3) k>2

問題５【標準】
　x の2次関数 y=(x−2k+1)2 のグラフについて，軸の方程式と頂点の座標を求めよ．また次の各場合についてグラフをかけ．
(1) k<12　(2) k=12　(3) k>12

問題６【標準】
　x の2次関数 y=x2+(2k−4)x のグラフについて，軸の方程式と頂点の座標を求めよ．

問題１【基本】

次の2次関数のグラフは，2次関数 y=2x2 のグラフをどのように移動したものか．また軸と頂点を求め，グラフをかけ．
(1) y=2x2−1　(2) y=2(x+3)2　(3) y=2(x+3)2−1　

　スライド や ノート では関数 y=ax2 のグラフからスタートして，y=ax2+q，y=a(x−p)2 とたどり，y=a(x−p)2+q に到達しました．

　y=ax2+q
　　→ y=ax2 を y 軸方向に q だけ平行移動
　y=a(x−p)2
　　→ y=ax2 を x 軸方向に p だけ平行移動
　y=a(x−p)2+q
　　→ y=ax2 を
　　　　　　x 軸方向に p，y 軸方向に q
　　　 だけ平行移動

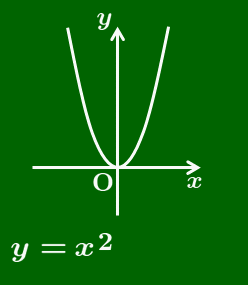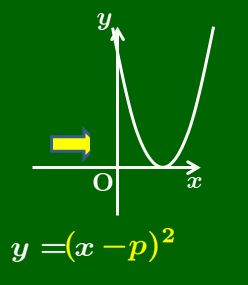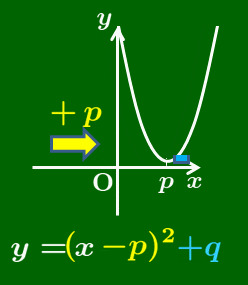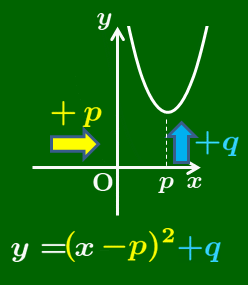
　3番目の変形は，1番目と2番目の表現を含んでいます．
　　1番目：3番目の p=0 の場合
　　2番目：3番目の q=0 の場合
　つまり1番目と2番目は，3番目の特別な場合を示しているにすぎません．
　また，2次関数のグラフを考える上では，上の3パターンが基本で，当面この3パターンだけで大丈夫ですが，数学Ⅱで学ぶ積分という分野では軸や頂点の情報よりもむしろ x 切片の方に興味があるため，y=a(x−α)(x−β) といった表現が好まれる場合があります．

解答

(１) y 軸方向に −1 だけ平行移動したもの．
　　軸は直線 x=0 ( y 軸)　頂点は点 (0,−1)

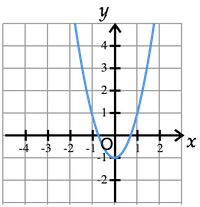
(2) x 軸方向に −3 だけ平行移動したもの．
　　軸は直線 x=−3　頂点は点 (−3,0)

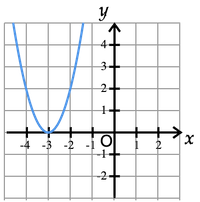
(3) x 軸方向に −3， y 軸方向に −1 だけ平行移動したもの．
　　軸は直線 x=−3　頂点は点 (−3,−1)

問題２【基本】

次の2次関数のグラフの軸と頂点を求め，グラフをかけ．
(1) y=2x2−4x+4　(2) y=−x2+2x　(3) y=12x2+2x+3

　y=ax2+bx+c の形のままでは，この放物線が座標平面上のどの位置にあるのかは分かりません．y=a(x−p)2+q の形になって初めてこの放物線の位置を捉えることができるのです．y=ax2+bx+c の形を変形してy=a(x−p)2+q の形にすることを 平方完成 というのでした．平方完成は2次関数を取り扱う上で必須です．いつでもスムーズにできるようにしておくことが大切です．

解答

(1)

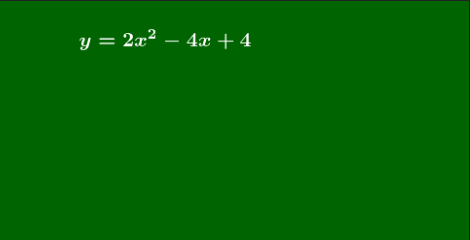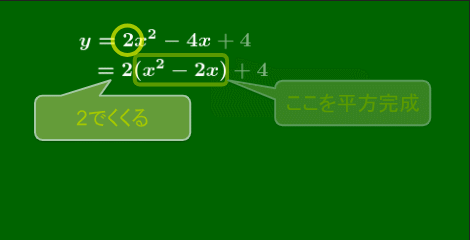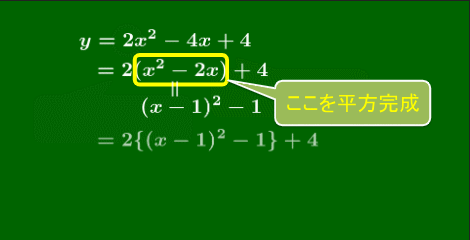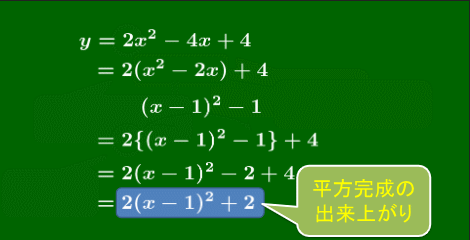
y=2x2−4x+4=⋯=2(x−1)2+2

　従って軸は　直線 x=1　頂点は点 (1,2)