整式を1次式で割った余りに関する定理が剰余の定理です.また剰余の定理で余りが0になる特別な場合に関しての主張が因数定理です.
3次以上の整式を因数分解する際の道具となるのが因数定理です.しかし3次以上の式の因数分解は,因数定理を知っていても多少の試行錯誤は必要で,場合のよっては大変な思いをさせられます.この節の最後に少し発展的な内容ではありますが,ある条件を満たした3次以上の整式を因数分解する際に非常に強力な取り扱い方を紹介します.
高校数学[総目次]
数学Ⅱ 第2章 複素数と方程式
| スライド | ノート | |
| 1. 複素数 | [無料] | |
| 2. 2次方程式の解と判別式 | [無料] | |
| 3. 解と係数の関係 | [会員] | |
| 4. 剰余の定理・因数定理 | [会員] | |
| 5. 高次方程式 | [会員] |

| 4.1 剰余の定理 | スライド① |
| 4.2 因数定理 | スライド② |
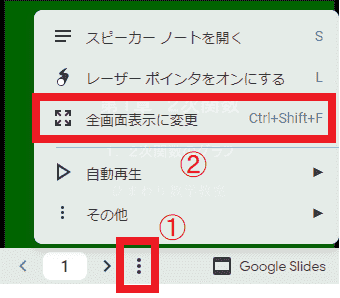
スライドはぜひ全画面表示で
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
