2.　2次方程式の解と判別式(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第2章　複素数と方程式

	スライド	ノート
1. 複素数	[無料]
2. 2次方程式の解と判別式	[無料]
3. 解と係数の関係	[会員]
4. 剰余の定理・因数定理	[会員]
5. 高次方程式	[会員]

2.　2次方程式の解と判別式

　このノートでは，方程式の係数や定数項は実数を仮定する．

2.1　解の公式

　$x$ の1次方程式 $ax+b=0\ (a\neq0)$ はどんなものでも $x=-\dfrac ba$ という具合に，方程式の解を係数 $a, b$ を用いて簡単に書き表すことができた．このように方程式の係数を用いて書き表された解を解の公式という．

　では2次方程式 $ax^2+bx+c=0$ についてはどうか．1次方程式 $ax+b=0$ から見れば式自体がかなり複雑だが，1次方程式と同様の係数 $a,b,c$ の式として解を書き表すことができるのであろうか？

　それを考える前にいくつかの2次方程式を実際に解いておこう．

例1　$2x^2-8=0$

　変形して

\[\begin{align*} x^2-4&=0\\[5pt] (x+2)(x-2)&=0\\[5pt] x&=\pm2 \end{align*}\]

例2　$x^2-4x-5=0$

　変形して

\[\begin{align*} (x+1)(x-5)&=0\\[5pt] x&=-1,5 \end{align*}\]

　これらの例では因数分解によって解を導くことができたが，別の方法によっても解を導くことができる．

例1の別解

　変形して

\[\begin{align*} x^2-4&=0\\[5pt] x^2&=4\\[5pt] x&=\pm2 \end{align*}\]

例2の別解

　変形して

\[\begin{align*} x^2-4x&=5\\[5pt] (x-2)^2-4&=5\\[5pt] (x-2)^2&=9\\[5pt] x-2&=\pm3\\[5pt] x&=2\pm3\\[5pt] x&=-1,\ 5 \end{align*}\]

　元の解き方に比べ，とりわけ例2では時間がかかったが，実はこの解き方の流れこそ2次方程式の解の公式を考える上でのヒントになるのだ．そこでこの解き方の流れをさらっておこう．

　この流れで一般の2次方程式 $ax^2+bx+c=0$ の解を導いてみよう．

Q. 　2次方程式 $ax^2+bx+c=0$ の解を求めよ．

A.

\[\begin{align*} ax^2+bx+c&=0\\[5pt] x^2+\frac bax+\frac ca&=0\\[5pt] x^2+\frac bax&=-\frac ca\\[5pt] \left(x+\frac b{2a}\right)^2-\frac{b^2}{4a^2}&=-\frac ca\ \ (\mbox{←平方完成})\\[5pt] \left(x+\frac b{2a}\right)^2&=\frac {b^2-4ac}{4a^2}\\[5pt] x+\frac b{2a}&=\pm\frac{\sqrt{b^2-4ac}}{2a}\\[5pt] \end{align*}\] \[\therefore \underline{\boldsymbol{x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}}}\]

補足

　$ax^2+2b\,’x+c=0$ のとき， \[\begin{align*} x&=\frac{-2b\,’\pm\sqrt{(2b\,’\,)^2-4ac}}{2a}\\[5pt] &=\frac{-2b\,’\pm2\sqrt{{b\,’\,}^2-ac}}{2a}\\[5pt] &=\underline{\boldsymbol{\frac{-b\,’\pm\sqrt{{b\,’\,}^2-ac}}{a}}} \end{align*}\]

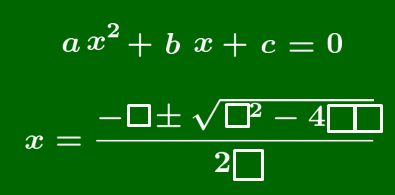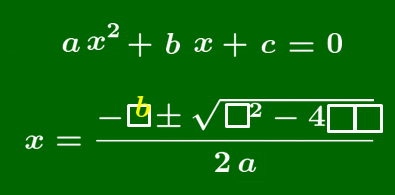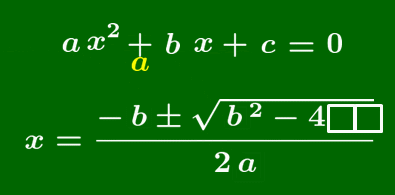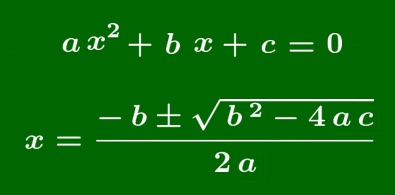
例題　次の2次方程式を解け．
(1) $x^2+5x-2=0$
(2) $3x^2-x+1=0$
(3) $x^2+6x-3=0$

こたえ

(1)

　解答例を表示する >

\[\begin{align*} x&=\frac{-5\pm\sqrt{5^2-4\cdot1\cdot(-2)}}{2\cdot1}\\[5pt] &=\underline{\boldsymbol{\frac{-5\pm\sqrt{33}}2}} \end{align*}\]

(2)

　解答例を表示する >

\[\begin{align*} x&=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot3\cdot1}}{2\cdot3}\\[5pt] &=\frac{1\pm\sqrt{-11}}6\\[5pt] &=\underline{\boldsymbol{\frac{1\pm\sqrt{11}\,i}6}} \end{align*}\]

(3)

　解答例を表示する >

\[\begin{align*} x&=\frac{-3\pm\sqrt{3^2-1\cdot(-3)}}1\\[5pt] &=-3\pm\sqrt{12}\\[5pt] &=\underline{\boldsymbol{-3\pm2\sqrt3}} \end{align*}\]

2.2　判別式

　次の3つの2次方程式を，解の公式を用いて解いてみよう．

　(1)は異なる2つの実数解をもち，(2)は1つの実数解 $-\dfrac12$ をもち，(3)は実数解がない．(2)のように2つの解が同じ値のとき，これを重解という．また(3)は実数解こそもたないが異なる2つの虚数解をもっている．

　この実数解の個数の違いはどこから生じてくるのであろうか？私たちはどこを見れば「実数解が2個ある」とか「重解である」などと判断できるのであろうか？それは

$\sqrt{\ \mbox{　　}}$ の部分だけを見れば判断できる

のである．$\sqrt{b^2-4ac}$ が実数ならば解は実数解となるが，それは $\sqrt{\ \mbox{　　}}$ の中身である $b^2-4ac$ が0以上であることと同値である．

　一般に2次方程式 $ax^2+bx+c=0$ の解は，解の公式により，

\[x-\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]

であるから，この方程式の解の種類は，$\sqrt{\mbox{　}}$ の中身である $b^2-4ac$ の値によって次のように決まる：

　　①　$b^2-4ac > 0\iff$ 異なる2つの実数解
　　②　$b^2-4ac = 0\iff$ 実数解は1個（重解）
　　③　$b^2-4ac < 0\iff$ 実数解は0個（異なる2つの虚数解）

　このように $b^2-4ac$ の値は2次方程式 $ax^2+bx+c=0$ の解の種類を判別する式であるからこれを判別式 (Discriminant) といい，$D$ で表される．

\[D=b^2-4ac\]

補足

　$ax^2+2b\,’x+c=0$ のときは， \[x=\frac{-b\,’\pm\sqrt{{b\,’\,}^2-ac}}a\] であったから，解の判別は ${b\,’\,}^2-ac$ でできる．これは判別式 $D=b^2-4ac\Bigl(=(2b\,’)^2-4ac\Bigr)$ の4分の1であるから，しばしば $D/4$ で表される：

\[D/4={b\,’\,}^2-ac\]

判別式　2次方程式 $ax^2\!+\!bx\!+\!c\!=\!0$ の解は，$D\!=\!b^2\!-\!4ac$ とすると， \[\left\{\begin{array}{l} D>0\iff \mbox{異なる2つの実数解をもつ}\\ D=0\iff \mbox{重解をもつ}\\ D<0\iff \mbox{異なる2つの虚数解をもつ} \end{array}\right.\] 　また，$ax^2\!+\!2b\,’x\!+\!c\!=\!0$ のときは，$D/4={b\,’\,}^2\!-\!ac$ とすると， \[\left\{\begin{array}{l} D/4>0\iff \mbox{異なる2つの実数解をもつ}\\ D/4=0\iff \mbox{重解をもつ}\\ D/4<0\iff \mbox{異なる2つの虚数解をもつ}\end{array}\right.\]

例題　次の2次方程式の解の種類を判別せよ．
(1)　$2x^2+3x+5=0$
(2)　$4x^2-12x+9=0$

答　判別式を $D$ とする．

(1)

　解答例を表示する >

\[D=3^2-4\cdot2\cdot5=-31< 0\] 　よって，異なる2つの虚数解をもつ．

(2)　　　

　解答例を表示する >

\[D/4=(-6)^2-4\cdot9=0\] 　よって，重解をもつ．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅱ　第2章　複素数と方程式

	スライド	ノート
1. 複素数	[無料]
2. 2次方程式の解と判別式	[無料]
3. 解と係数の関係	[会員]
4. 剰余の定理・因数定理	[会員]
5. 高次方程式	[会員]