高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |

7.曲線の媒介変数表示
7.1 媒介変数表示
まずは例から
これまで直線や曲線といえば,例えば y=x+1 や y=x2 のようなものがあった.ここでは,直線や曲線を別のやり方で表現する考え方を学ぶ.
例として直線 y=x+1 を考えよう.
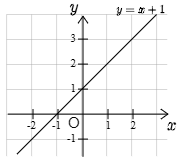
この直線上の点をいくつか拾ってくると,
x=−1 のとき,y=0 よって点(−1, 0)
x= 0 のとき, y=1 よって点 (0, 1)
x= 1 のとき, y=2 よって点 (1, 2)
x= 2 のとき, y=3 よって点 (2, 3)
⋮
などがある.ここで,実数 t を用いて例えば x=t2 とおいてみると,y=x+1 より y=t2+1 であるから,
t=−1 のとき,x=1, y=2 よって点 (1, 2)
t= 0 のとき, x=0, y=1 よって点 (0, 1)
t= 1 のとき, x=1, y=2 よって点 (1, 2)
t= 2 のとき, x=4, y=5 よって点 (4, 5)
⋮
などとなっている.
x 座標を決めたのちに y 座標が決まるという y=x+1 が言わば, x と y の直接的な関係を記したものであるのに対し,
{x=t2y=t2+1 …①
という表現は,点 (x, y) を動かす原動力である t を仲立ちにして,この t を動かすことで直線や曲線を与えるのである.
とはいっても,①の表現の仕方では直線 y=x+1 の x≧0 の部分しか表せない.x=t2≧0 となるからである.従って①で表される図形は半直線である.このように x と y を t でどのように表すかで図形の範囲が制限されることもある.あるいは制限できるようになった,と言った方がよいかもしれない.またすぐ上で確認したように,t の値が同じ1だけ増加するといっても,−1 から 0 へ増加する場合は,点が (1, 2) から (0, 1) へと左下に移動し,t が 0 から 1 へと増加する場合は,点が (0, 1) から (1, 2) へと右上に移動している.すなわち x や y を上手く t で表すことで,点が図形上を行ったり来たりと動き方の制御ができるようになるのである.

それでは一般論
一般に,平面上の曲線 C が,変数 t によって
x=f(t), y=g(t)
の形に表されるとき,これを曲線 C の媒介変数表示,またはパラメータ表示という.また,変数 t を媒介変数,またはパラメータという.
例題 x=t−1, y=t2−2t で表される図形 C はどのようなものか.
こたえ
解答例を表示する
7.2 放物線の媒介変数表示
y2=4px (⋯①) より x=y24p.
よって,t を実数として y=2pt とおくと,y は実数全体をとり,x=pt2.従って①の媒介変数表示の1つは
(pt2, 2pt)
放物線 y2=4px の媒介変数表示 (pt2, 2pt)
例題 y2=4x について,上と同様の媒介変数表示をせよ.
こたえ
解答例を表示する
7.3 円の媒介変数表示
原点Oを中心とする円 x2+y2=a2 (⋯①) 上の点をP(x,y) とし,動径OPの表す一般角を θ とすると,三角関数の定義から
x=acosθ, y=asinθ
これは,円①の媒介変数表示となっている.
円 x2+y2=a2 の媒介変数表示 (acosθ, asinθ)
例題 円 x2+y2=4 について,上と同様の媒介変数表示をせよ.
こたえ
解答例を表示する
7.4 楕円の媒介変数表示
楕円 x2a2+y2b2=1 (⋯①) 上の点 (x,y) に対し,
X=xa, Y=yb
とおくと,①は
X2+Y2=1
と表される.これは点 (X,Y) が円 x2+y2=1 上の点であることを意味するから,すぐ上で学習したように原点を中心とする半径1の円の媒介変数表示から
X=cosθ, Y=sinθ
と表せる.よって xa=cosθ, yb=sinθ より,
x=acosθ, y=bsinθ
楕円 x2a2+y2b2=1 の媒介変数表示 (acosθ, bsinθ)
例題 楕円 x216+y24=1 について,上と同様の媒介変数表示をせよ.
こたえ
解答例を表示する
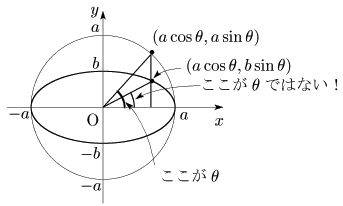
重要な注意
θ の位置に注意すること.

7.5 双曲線の媒介変数表示
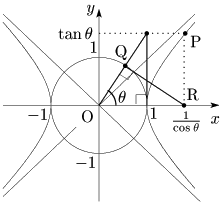
三角関数の公式より,
1+tan2θ=1cos2θ
∴1cos2θ−tan2θ=1
よって,点 (1cosθ, tanθ) ⋯① は,双曲線 x2−y2=1 上にある.
一方,単位円周上の点 Q(cosθ,sinθ) に対して,上の図のように点Pをとると,Pの座標は①で表される.
Pの位置は θ によって次のようになる:
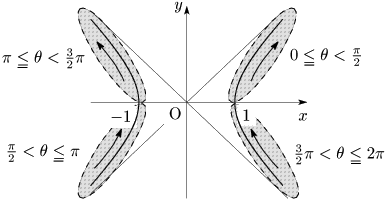
双曲線 x2a2−y2b2=1 で,X=xa, Y=yb とおくと,X2−Y2=1.よって,点 (X,Y) は①で表されるから,xa=1cosθ, yb=tanθ より
(x,y)=(acosθ, btanθ)
双曲線 x2a2−y2b2=1 の媒介変数表示 (acosθ, btanθ)
例題 双曲線 x29−y24=1 について,上と同様の媒介変数表示をせよ.
こたえ
解答例を表示する
7.6 媒介変数で表された曲線の平行移動
曲線 x=f(t), y=g(t) を、x 軸方向に p,y 軸方向に q だけ平行移動した曲線の媒介変数表示は x=f(t)+p, y=g(t)+q
例題 x=2cosθ+3, y=2sinθ+1 で表される曲線はどのようなものか.
こたえ
解答例を表示する
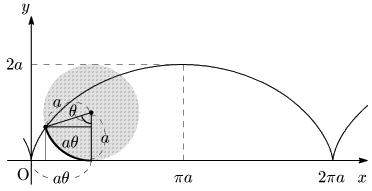
7.7 サイクロイド

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |

