高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |

6.2次曲線の性質
放物線,楕円,双曲線の3つの曲線は,
- 放物線:定点と定直線から等距離にある点の軌跡
- 楕円:2点からの距離の和が一定である点の軌跡
- 双曲線:2点からの距離の差が一定である点の軌跡
として導入された.出発点である定義が異なるのだから,これらの曲線たちはそれぞれに形状が異なっているのは当然である.ところが驚くべきことに,放物線,楕円,双曲線という3つの曲線には背後に潜む共通項とでもいうべきものが存在しており,これら3つの曲線を上で定義した方法とは全く別の,ある1つの統一的な視点から導入し直すことが可能なのだ.タイトルの「2次曲線の性質」とは,今まさに明るみに出ようとしていその共通項を指す.
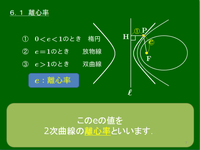
6.1 離心率
2次曲線を統一的な視点から捉え直す
原点Oを通らない定直線 ℓ を x=k,点P(x,y) から ℓ に下ろした垂線の足をHとする. OP:PH=e:1 (e>0) となる点Pの軌跡を考えよう.
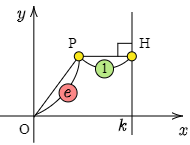
OP:PH=e:1⟺OP=ePH⟺√x2+y2=e|x−k|⟺x2+y2=e2(x−k)2⟺(1−e2)x2+y2+2e2kx−e2k2=0
従って
- 0<e<1 のとき
x2 と y2 の係数が同符号になるから楕円 - e=1 のとき
x2 の項が落ちるから放物線 - e>1 のとき
x2 と y2 の係数が異符号になるから双曲線
となることがわかる.(x2 と y2 の項以外は概形を決定付けない.)
一般に,定点Fと,Fを通らない直線 ℓ からの距離の比が FP:PH=e:1 (e>0) となる点Pの軌跡は次のようになる:
① 0<e<1 のとき 楕円
② e=1 のとき 放物線
③ e>1 のとき 双曲線
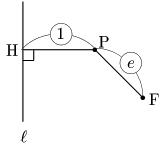
e の値を2次曲線の離心率(eccentricity),直線 ℓ を準線(directrix)という.
覚え方
FP:PHが e:1 なのであるが,e:1 だったか 1:e だったかよく忘れてしまう.そこで覚え方.
近所の良い商店
(e 焦点)
e に近い方が焦点だという意味.


原点と x 軸に垂直な直線からの距離の比
例題 原点Oと直線 x=3 からの距離の比が一定で,e:1 である点Pの軌跡 C を,
[1] e=12 [2] e=1 [3] e=2
の各場合について求めよ.
こたえ
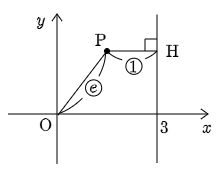
OP:PH=e:1 より,OP=ePH
両辺を2乗して OP2=e2PH2
よって x2+y2=e2|x−3|2
整理して (1−e2)x2+y2+6e2x−9e2=0 ⋯①
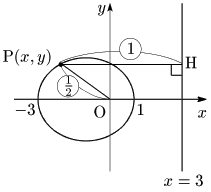
[1] e=12 のとき
①に代入して整理すると (x+1)24+y23=1
よって C は楕円 x24+y23=1 を x 軸方向に −1 だけ平行移動した楕円.
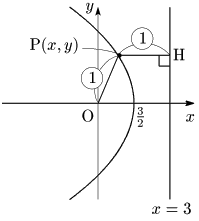
[2] e=1 のとき
①に代入して整理すると y2=−6(x−32)
よって C は放物線 y2=−6x を x 軸方向に 32 だけ平行移動した放物線.
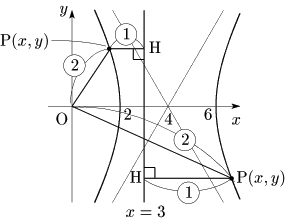
[3] e=2 のとき
①に代入して整理すると (x−4)24−y212=1
よって C は双曲線 x24−y212=1 を x 軸方向に 4 だけ平行移動した双曲線.
補足
双曲線は1定点と1直線で,2つの曲線が描ける
双曲線は2つの曲線が対になっているが,すぐ上の図を見ればわかるように1つの焦点と対応する準線1本で2つの曲線が共に描かれる.

6.2 標準形と離心率
標準形で表された2次曲線の離心率と準線
y2=4px や x2a2+y2b2=1 などの標準形で与えられた2次曲線に対して,その離心率と準線はどのように表されるのだろうか。放物線 y2=4px は離心率が1,準線が直線 x=−p とすぐにわかるからよいとして,問題は楕円と双曲線である.これらの場合を以下で調べるのであるが,いずれの場合も
焦点と曲線上の点の距離を計算すると,その結果に離心率と準線が自然と現れる
というのがポイントである.ついでに述べておくと,2点間の距離を計算する際に現れる根号は外れないことも多いが,標準形で表された2次曲線の場合は中身が平方式になって根号が外れることもぜひ覚えておきたい.
楕円
楕円 x2a2+y2b2=1 (a>b>0) 上の点をP(x,y),焦点の1つをF(c,0) とする.(c=√a2−b2)
FP=√(x−c)2+y2=√(x2−2cx+c2)+(−b2a2x2+b2)=√a2−b2a2x2−2cx+(b2+c2)=√c2a2x2−2cx+a2 (∵c=√a2−b2)=√(cax−a)2=|cax−a|=ca|x−a2c|
よって,直線 ℓ を x=a2c とし,Pから ℓ に下ろした垂線の足をHとすると,
FP=caPH
∴FP:PH=ca:1
従って離心率 e=ca=√a2−b2a である.
またこのときの e を用いると,c=ae より
準線 ℓ:x=a2c=ae
焦点:(ae,0)
となる.また対称性により,
準線 ℓ:x=−a2c=−ae
焦点:(−ae,0)
の組もある.
まとめ
楕円 x2a2+y2b2=1 (a>b>0) において,
離心率 e=√a2−b2a
焦点 (±ae,0)
準線 x=±ae
(複号同順)
双曲線
双曲線 x2a2−y2b2=1 (a>0,b>0) 上の点をP(x,y),焦点の1つをF(c,0) とする.(c=√a2+b2)
FP=√(x−c)2+y2=√(x2−2cx+c2)+(b2a2x2−b2)=√a2+b2a2x2−2cx+(c2−b2)=√c2a2x2−2cx+a2 (∵c=√a2+b2)=√(cax−a)2=|cax−a|=ca|x−a2c|
従って離心率 e=ca=√a2+b2a である.
またこのときの e を用いると,c=ae より
準線 ℓ:x=a2c=ae
焦点:(ae,0)
となる.また対称性により
準線 ℓ:x=−a2c=−ae
焦点:(−ae,0)
の組もある.
まとめ
双曲線 x2a2−y2b2=1 (a>0,b>0) において,
離心率 e=√a2+b2a
焦点 (±ae,0)
準線 x=±ae
(複号同順)

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |