5．2次曲線と直線(ノート)｜スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート	問題
1. 放物線	[会員]
2. 楕円	[会員]
3. 双曲線	[会員]
4. 2次曲線の平行移動	[会員]
5. 2次曲線と直線	[会員]		[会員]
6. 2次曲線の性質	[会員]
7. 曲線の媒介変数表示	[会員]
8. 極座標と極方程式	[会員]

5．2次曲線と直線

5.1 2次曲線と直線の共有点

共有点の個数を求める際の考え方は，これまでと何ら変わらない

　2次曲線と直線の共有点を考察するにあたって，これまでにない何か特別なことがある訳ではない．基本的には $x$ か $y$ のどちらかの文字を消去して2次方程式を作り，その解の種類，個数を考察するのである．しかし楕円に関しては，下の例題にある通り楕円と円の親戚関係を利用することで，計算が大幅にラクになる場合がある．

直線との共有点の個数の求め方放物線：連立して判別式
楕　円：連立して判別式
双曲線：直線と漸近線が平行でない
　　　　　→放物線・楕円の-ケースと同じ
　　　　直線と漸近線が平行
　　　　　→漸近線そのもの→0個
　　　　　→それ以外→1個

例題1　双曲線 $\dfrac{x^2}{12}-\dfrac{y^2}3=1$ と直線 $y=x+k$ の共有点の個数を求めよ．

補足

　$D=0$ のとき，接するという．漸近線に平行な直線は接線になり得ない．

楕円の場合は円との親戚関係を用いた上手い考え方がある

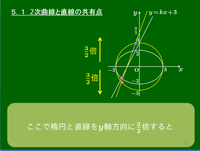
例題2　楕円 $\dfrac{x^2}9+\dfrac{y^2}4=1$ と直線 $y=kx+3$ の共有点の個数を求めよ．

方針
例題1と同様に解決できるが，楕円と円の関係を用いた次の解法がおすすめ．

5.2 2次曲線の接線の方程式

2次曲線上の点における接線の方程式には公式がある

　2次曲線上の点 $(x_1,\ y_1)$ 上における接線の方程式は次で与えられる：

2次曲線の接線の方程式 接点の座標が $(x_1,y_1)$ のとき，
　①放物線 $y^2=4px \to y_1y=2p(x+x_1)$
　②楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 \to \dfrac{x_1x}{a^2}+\dfrac{y_1y}{b^2}=1$
　③双曲線 $\left\{ \begin{array}{ll} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 &\to \dfrac{x_1x}{a^2}-\dfrac{y_1y}{b^2}=1\\[5pt] \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1 &\to \dfrac{x_1x}{a^2}-\dfrac{y_1y}{b^2}=-1 \end{array}\right.$

覚え方
　①放物線　$2x\to x+x_1,\ y^2\to y_1y$
　②③楕円，双曲線　　$x^2\to x_1x,\ y^2\to y_1y$

証明

　数学Ⅲの微分法を用いる証明が最もはやいが，それでなければ次の方法が明快．

　点 $(x_1,y_1)$ を通り，方向ベクトルが $(\alpha,\beta)$ である直線 $\ell$ のベクトル方程式は，$t$ を実数として $$(x,y)=(x_1,y_1)+t(\alpha,\beta)$$ $$\therefore\left\{\begin{array}{l} x=x_1+\alpha t\\[5pt] y=y_1+\beta t \end{array}\right.\ \ \cdots(*)$$ と表せる．この直線が2次曲線上の点 $(x_1,\ y_1)$ における接線となるとき，$x,y$ を消去して得られる $t$ の2次方程式が $\boldsymbol{t=0}$ を重解にもつ．(さもなくば，$t=0$ 以外の $t$ に対応する点で，2次曲線と直線が共有点をもち，接していないことになる．)

①　放物線

　$y^2=4px$ に $(*)$ を代入して，
$$\begin{align} (y_1+\beta t)^2&=4p(x_1+\alpha t)\\[5pt] {y_1}^2+2y_1\beta t+\beta^2t^2&=4px_1+4p\alpha t\\[5pt] \end{align}$$
　${y_1}^2=4px_1$ に注意して整理すると，

$\beta^2t^2-2(2p\alpha-y_1\beta)t=0$　…①

　2次の係数 $\beta^2$ について，$\beta=0$ とすると，直線の方向ベクトルが $(\alpha,\ 0)$ となり，直線は $x$ 軸と平行になるが，放物線 $y^2=4px$ の接線にそのようなものはないので $\beta\neq0$ である．よって①は $t$ の2次方程式である．$\ell$ が放物線の接線のとき，この2次方程式が $t=0$ を重解にもつから，
$$\begin{align} 2p\alpha-y_1\beta&=0\\[5pt] \therefore (2p,-y_1)\cdot(\alpha,\beta)&=0 \end{align}$$ 　従ってベクトル $(2p,\ -y_1)$ は，$\ell$ の方向ベクトル $(\alpha,\beta)$ と垂直であるから，$\ell$ の法線ベクトルとなる．よって，接線の方程式は， $$\begin{align} 2p(x-x_1)-y_1(y-y_1)&=0\\[5pt] 2\,p\,x-2\,p\,x_1-y_1\,y+y_1^2&=0\end{align}$$

　${y_1}^2=4px_1$ であるから $$2\,p\,x-2\,p\,x_1-y_1y+4\,p\,x_1=0$$ $$\therefore y_1y=2p(x+x_1)$$

②，③　楕円，双曲線

　曲線 $C$ の方程式を，$p>0$，$q\neq0$ として

$$C:p\,x^2+q\,y^2=1$$

とおく．$q>0$ のときは楕円で，$q<0$ のときは双曲線を表す．$C$ 上の点を $(x_1,y_1)$ とし，$(*)$ を代入すると，

$$p(x_1+\alpha t)^2+q(y_1+\beta t)^2 =1$$

　展開して $t$ について整理すると，$p{x_1}^2+q{y_1}^2=1$ にも注意して

$$(p\alpha^2+q\beta^2)t^2+2(p\,\alpha\, x_1+q\,\beta \,y_1)t =0$$

　$t^2$ の係数 $p\,\alpha^2+q\,\beta^2$ について，これが0でないことを確認しておこう．$(\alpha,\ \beta)$ は $\ell$ の方向ベクトルだからもちろん $(\alpha,\ \beta)\neq\overrightarrow0$．$p>0$ と仮定しておいたから， $q>0$ のときは $p\,\alpha^2+q\,\beta^2\neq0$．また $q<0$ の場合でも，$p\,\alpha^2+q\,\beta^2=0$ となるときは，$\ell$ の方向ベクトル $(\alpha,\ \beta)$ が双曲線の漸近線の方向ベクトル $(\sqrt{-q},\ \pm\sqrt{p})$ と平行になってしまうから不適．以上により $p\,\alpha^2+q\,\beta^2\neq0$ であることがわかった．

　よって $\ell$ が2次曲線の接線のとき，この $t$ の2次方程式が $t=0$ を重解にもつから，

$$\begin{align} p\,\alpha\, x_1+q\,\beta\, y_1&=0\\[5pt] (\alpha,\ \beta)\cdot(p\,x_1,\ q\,y_1)&=0 \end{align}$$

　よって，$(\alpha,\ \beta)\perp(p\,x_1,\ q\,y_1)$ であるから，ベクトル $(p\,x_1,\ q\,y_1)$ は接線の法線ベクトルとなる．

　ベクトル $(p\,x_1,\ q\,y_1)$ について，これが $\overrightarrow0$ でないことを確認しておこう．$p>0$ であるから $x_1\neq0$ のときは $(p\,x_1,\ q\,y_1)\neq\overrightarrow0$．また，$x_1=0$ のときは $p\,{x_1}^2+q\,{y_1}^2=1$ から $y_1\neq0$ だから，このときも $(p\,x_1,\ q\,y_1)\neq\overrightarrow0$．以上により，$(p\,x_1,\ q\,y_1)\neq\overrightarrow0$ であることがわかった．

従って接線の方程式は，

$$p\,x_1(x-x_1)+q\,y_1(y-y_1)=0$$

整理して，$p{x_1}^2+q{y_1}^2=1$ を用いると，

$$px_1x+qy_1y=1$$

補足

数学Ⅲの微分が使えれば，その場での導出もたやすい

　数学Ⅲの微分法を用いると次のように示される：

①　放物線

　$y^2=4px$ の両辺を $x$ で微分して　$2yy’=4p$
　$y\neq0$ のとき，$y’=\dfrac{2p}y$．
　従ってこのとき接線の方程式は，
$$\begin{align} y-y_1&=\frac{2p}{y_1}(x-x_1)\\[5pt] \therefore y_1y&=2p(x-x_1)+{y_1}^2\\[5pt] \therefore y_1y&=2p(x+x_1)\ \ (\because {y_1}^2=4px_1)\\[5pt] \end{align}$$

　頂点 $(0,0)$ における接線の方程式は $x=0$ であるが，上の式で $(x_1,y_1)=(0,0)$ とおくと $x=0$ となるから，上の式はこの場合も含まれる．

②　楕円

　楕円 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ の両辺を $x$ で微分して $$\frac{2x}{a^2}+\frac{2yy’}{b^2}=0$$ 　$y\neq0$ のとき　$y’=-\dfrac{b^2x}{a^2y}$
　従ってこのとき接線の方程式は， $$y-y_1=-\dfrac{b^2x_1}{a^2y_1}(x-x_1)$$
　両辺を $\dfrac{y_1}{b^2}$ 倍して
$$\begin{align} \frac{y_1y}{b^2}-\frac{{y_1}^2}{b^2}&=-\frac{x_1}{a^2}(x-x_1)\\[5pt] \therefore \frac{x_1x}{a^2}+\frac{y_1y}{b^2}&=1\ \ (\because \frac{{x_1}^2}{a^2}+\frac{{y_1}^2}{b^2}=1) \end{align}$$
　$(x_1,y_1)=(\pm a,0)$ における接線の方程式は $x=\pm a$ (複号同順)だから，上の式はこの場合も含まれる．

③　双曲線

　②の楕円の場合と同様にして示される．

例題　点 $(0,3)$ から楕円 $x^2+4y^2=4$ に引いた接線の方程式，及び接点の座標を求めよ．

高校数学[総目次]

数学Ⅲ　第5章　2次曲線

	スライド	ノート	問題
1. 放物線	[会員]
2. 楕円	[会員]
3. 双曲線	[会員]
4. 2次曲線の平行移動	[会員]
5. 2次曲線と直線	[会員]		[会員]
6. 2次曲線の性質	[会員]
7. 曲線の媒介変数表示	[会員]
8. 極座標と極方程式	[会員]