高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |
1．放物線
数学Ⅰでは関数 $y=ax^2+bx+c$ のグラフを放物線といったが，ここでは2次曲線という枠組みの中で新たに定義し直す．
1.1 放物線の方程式
2次曲線という枠組みの中での放物線とは
放物線とは?
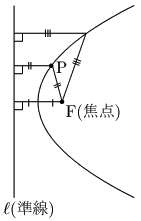
定点Fと，Fを通らない定直線$\ell$からの距離が等しい点Pの軌跡．
定点Fを焦点といい，定直線$\ell$を準線という．
補足
放物線が横を向いているのは何故か
放物線が横を向いたようになっていて違和感があるかもしれない．このあと続く楕円(及び円)，双曲線とあわせて2次曲線というが，これらは「定点と定直線からの距離の比が一定である点の軌跡」という形で統一した表現がとれる．この定直線を縦に伸びる直線としたために，放物線がしわ寄せを受けたというわけである．詳しくは 6節 2次曲線の性質 参照
焦点$(p,0)$，準線$x=-p$ の放物線
放物線の定義から方程式を導出する
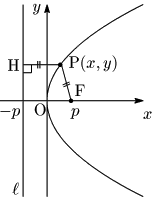
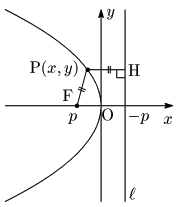
図において，
\[\begin{align*} {\rm PF}&={\rm PH}\ \ \cdots\ \mbox{①}\\[5pt] {\rm PF}^2&={\rm PH}^2\\[5pt] (x-p)^2+y^2&=|x-(-p)|^2\\[5pt] \therefore y^2&=4px\ \ \cdots\ \mbox{②} \end{align*}\]
よって条件①を満たす点は，曲線②上にある．逆に曲線②上の任意の点は，上の計算の逆をたどることで条件①を満たす．
方程式②を，放物線の方程式の標準形という．
まとめ $p\neq0$ とする．
焦点 $(p,0)$，準線 $x=-p$ である放物線の方程式は\[y^2=4px\]
発展的補足
放物線上の任意の点から焦点までの距離は，ルートがつかない
平面上の2点 $(x_1,\ y_1),\ (x_2,\ y_2)$ の距離は，$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$ で計算され，通常ルート $\sqrt{\hspace{6mm}}$ は外れないことが多い．しかし，放物線上の任意の点からこの放物線の焦点までの距離は，例外的にルートがつかない式として表すことができるのである．もう一度放物線の方程式 $y^2=4px$ を導出する過程を見てみよう．
\[\begin{align*} {\rm PF}&={\rm PH}\\[5pt] {\rm PF}^2&={\rm PH}^2\\[5pt] (x-p)^2+y^2&=|x-(-p)|^2\\[5pt]y^2&=4px\end{align*}\]
最初の ${\rm PF}={\rm PH}$ は
\[\sqrt{(x-p)^2+y^2}=|x+p|\]
と表される．すなわち放物線上の任意の点P$(x_1,\ y_1)$ と焦点F$(p,\ 0)$ までの距離 $\sqrt{(x_1-p)^2+{y_1}^2}$ は，$|x_1+p|$ で表されるのである．
実はこのあと登場する楕円や双曲線にも焦点と呼ばれる点があり，この点から楕円や双曲線上の点までの距離は，ルートの中身が同じように平方式となって，ルートが外れるのである．この事実は難関大入試問題で，曲線上の2点と焦点を結んだ三角形を考えさせる問題などで活躍する場合がある．
例題1 放物線 $y^2=x$ の焦点と準線を求めよ．
こたえ
解答例を表示する例題2 焦点が点 $(1,0)$，準線が直線 $x=-1$ である放物線の方程式を求めよ．
こたえ
解答例を表示する
1.2 $y$ 軸を軸とする放物線
数学Ⅰでやった形も当然表現できる
$p\neq0$ とする．点F $(0,p)$ を焦点とし，直線 $y=-p$ を準線とする放物線の方程式は
\[x^2=4py\]
例題 放物線 $y=2x^2$ の焦点と準線を求めよ．
こたえ
解答例を表示する
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第5章 2次曲線
| スライド | ノート | 問題 | |
| 1. 放物線 | [会員] | ||
| 2. 楕円 | [会員] | ||
| 3. 双曲線 | [会員] | ||
| 4. 2次曲線の平行移動 | [会員] | ||
| 5. 2次曲線と直線 | [会員] | [会員] | |
| 6. 2次曲線の性質 | [会員] | ||
| 7. 曲線の媒介変数表示 | [会員] | ||
| 8. 極座標と極方程式 | [会員] |