高校数学[総目次]
数学A 第2章 確率
| スライド | ノート | |
| 1. 事象と確率 | [無料] | |
| 2. 確率の基本性質 | [無料] | |
| 3. 独立な試行の確率 | [会員] | |
| 4. 反復試行の確率 | [会員] | |
| 5. 条件付き確率 | [会員] |

2. 確率の基本性質
2.1 積事象と和事象
全事象を表す集合を U,事象 A,B を表す U の部分集合をそれぞれ A,B とする.
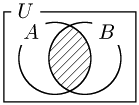
積事象
「事象 A,B がともに起こる」という事象で,
A∩B
で表す.
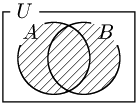
和事象
「事象 A または B が起こる」という事象で,
A∪B
で表す.

2.2 排反事象
例 さいころを1回だけ投げる場合
事象A:奇数の目が出る → A={1,3,5}
事象B:2の目が出る → B={2}
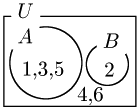
この2つの事象は同時には起こらない.このとき,事象AとBは互いに排反であるという.
即ち排反とは,A∩B=∅ となるときをいう.

2.3 確率の基本性質
全部の場合 :n 通り(同様に確からしい)
事象Aの起こる場合:a 通り
0≦a≦n であるから,
0n≦an≦nn ∴0≦P(A)≦1
補足
左辺の 0n 即ち 0 は空事象の確率,右辺の nn 即ち 1 は全事象の確率を表す.
確率の基本性質 U を全事象,A をある事象とするとき,[1] 0≦P(A)≦1[2] P(∅)=0, P(U)=1

2.4 和事象の確率
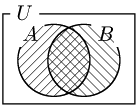
n(A∪B)=n(A)+n(B)−n(A∩B)
この両辺を n(U) で割ると,
n(A∪B)n(U)=n(A)n(U)+n(B)n(U)−n(A∩B)n(U)
∴P(A∪B)=P(A)+P(B)+P(A∩B)
特に,事象 A と事象 B が同時に起こらない,すなわち排反のとき,A∩B=∅ であるから,P(A∩B)=0.よって,
P(A∪B)=P(A)+P(B)
和事象の確率 2つの事象 A, B について,P(A∪B)=P(A)+P(B)−P(A∩B) 特に A と B が排反のとき,P(A∪B)=P(A)+P(B)
例題 さいころを1回投げるとき,偶数の目が出る,または4以上の目が出る確率を求めよ.
答
全事象U:U={1,2,3,4,5,6}
事象A「偶数の目が出る」:A={2,4,6}
事象B「4以上の目が出る」:B={4,5,6}
事象AかつB「偶数かつ4以上」:A∩B={4,6}
確率はそれぞれ P(A)=36=12P(B)=36=12P(A∩B)=26=13 よって, P(A∪B)=P(A)+P(B)−P(A∩B)=12+12−13=23_
補足
直接計算すれば,A∪B={2,4,5,6} より, P(A∪B)=46=23_

2.5 余事象の確率
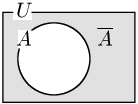
事象 A に対して,A が起こらないという事象を A の余事象といい,¯A で表す.
A∩¯A=∅ により P(A∩¯A)=0 であるから,
P(A∪¯A)=P(A)+P(¯A)
また全事象を U とすると,A∪¯A=U であるから左辺は1となり,次の関係を得る:
P(A)=1−P(¯A)
例題 2つのさいころを同時に投げるとき,次の確率を求めよ.
(1) 出た目の和が4にならない.
(2) 出た目の積が偶数.
ポイント
「⋯ ではない確率」(否定的表現)
「少なくとも ⋯ である確率」
→ 余事象の確率を考えてみる.
(1) 和が4にならない事象を A とすると,¯A は「和が4になる」という事象である.
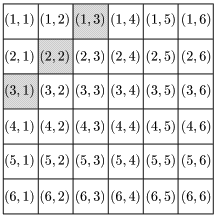
P(¯A)=336=112
よって求める確率 P(A) は,
P(A)=1−P(¯A)=1−112=1112_
(2) 積が偶数になるのは,「少なくとも一方の目が偶数」のときである.この余事象は,「両方とも奇数の目が出る」であるから,余事象の確率は,936=14.
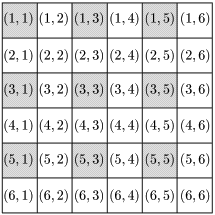
従って求める確率は,
1−14=34_

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第2章 確率
| スライド | ノート | |
| 1. 事象と確率 | [無料] | |
| 2. 確率の基本性質 | [無料] | |
| 3. 独立な試行の確率 | [会員] | |
| 4. 反復試行の確率 | [会員] | |
| 5. 条件付き確率 | [会員] |

