1. 事象と確率(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率	[無料]
2. 確率の基本性質	[無料]
3. 独立な試行の確率	[会員]
4. 反復試行の確率	[会員]
5. 条件付き確率	[会員]

1. 事象と確率

　確率という言葉はニュースなどでもよく見聞きする用語であるから，小学生，あるいはそれ以前から確率というものついて何となく意味は分かっているであろう．しかし数学的に「確率とは何か」ということを学ぶのは実はここが初めてである．数学的な確率を導入するに当たり，準備としていくつかの用語を説明していく．

1.1　試行と事象

　以下の用語は今後確率を説明するうえで繰り返し用いられるものばかりである．

試行

　同じ条件・状態の下でできる実験や観察

事象

　試行によっておこる事柄

根元事象	さいころを1回投げたとき，「1の目が出る」といった，もうそれ以上分解できない事象． （「偶数の目が出る」は根元事象ではない．）
全事象または 標本空間	1つの試行における根元事象全体の集合
空事象	決して起こらない事象．$\varnothing$ で表される

　事象と集合は完全に対応している．以後，全体集合 $U$ の部分集合$A$ と事象A を区別しないで同じものを表しているものとする．

例　さいころを1回だけ投げて，出た目を調べる．

　試行　：さいころを1回だけ投げる
　根元事象：
　　　1の目が出る→ $\{1\}$ で表す．
　　　2の目が出る→ $\{2\}$ で表す．
　　　3の目が出る→ $\{3\}$ で表す．
　　　4の目が出る→ $\{4\}$ で表す．
　　　5の目が出る→ $\{5\}$ で表す．
　　　6の目が出る→ $\{6\}$ で表す．
　全事象(または標本空間)：
　　　集合 $\{1,2,3,4,5,6\}$ で表される．
　空事象：
　　　例　7の目が出る．
　　　　　この事象に対応する集合を $E$ とすれば，
　　　　　　　　$E=\varnothing$

発展的補足~事象とは？

　「事象とは何か？」ということを難しく言えば，それは全事象(あるいは標本空間)という名の集合の，部分集合のことである．この例の場合の全事象(標本空間)は $\{1,2,3,4,5,6\}$ という集合であり，例えば「偶数の目が出るという事象」とは，全事象(標本空間)の部分集合 $\{2,4,6\}$ を意味するのである．このように確率論では「事象＝集合」という関係が本質的であって，この言い方の方がかえってしっくりくるという向きもあろう．

1.2　確率

確率を計算するうえで極めて重要な「同様に確からしい」

同様に確からしい　(←用語)

　根元事象のどれについても，起こることが同程度に期待されること．特定の事象が出やすいとか出にくいということがないときをいう．

例　さいころ1回投げ
　1～6の目の出方は，同程度であると期待される．(1が出やすいとか，6が出にくいということがない．)　よって，さいころの目の出方は同様に確からしいといえる．

確率とは何か？

　確率というと，天気予報の降水確率や宝くじの当選確率など割と身近なところで用いられてきた．数学における確率も意味としてはほぼ同じで，「…が起こる割合」という理解でひとまず問題ないが，いろいろと細かな注意点もある．

　ある試行で起こり得るすべての場合が $n$ 通りあり，そのどれもが同様に確からしいとする．このうち事象Aの起こる場合が $a$ 通りであるとき， $$\frac an$$ を事象Aの起こる確率といい，$\boldsymbol P(A)$ で表す：

確率の定義　ある試行で起こりうることが全部で $n$ 通りあり，そのどれもが同様に確からしいとする．このうち，事象 $A$ の起こる場合が $a$ 通りであるとき，事象 $A$ が起こる確率 $P(A)$ は $$P(A)=\frac an$$

注意

　数学における確率について，いくつか注意をしておく．

①「同様に確からしい」は必須の要件

　確率が $\dfrac an$ で計算できるのは，分母の $n$ 通りが同様に確からしい場合であって，この要請は絶対である．同様に確からしくなければこの式は使えない．例えば，2枚のコインを同時に投げたとき，表(おもて)が出る枚数は0，1，2の3通りのいずれかであるが，2枚とも表である確率は $\dfrac13$ ではない．事象 $\{0\}$，$\{1\}$，$\{2\}$ の起こり方が同様に確からしくないからである．正しい確率は $\dfrac14$ である．

②確率は0以上1以下で定義されている．

　この確率の定義から，
　事象 $A$ が全く起こらなければ，$P(A)=\dfrac0n=0$
　事象 $A$ が常に起こるならば，$P(A)=\dfrac nn=1$
である．つまり，数学における確率の値は0以上1以下である．お馴染みの百分率で表すと，確率0は0%，確率1は100%である．ある球団の熱烈なファンが「今夜は120%勝つ！」と息巻く姿を時折目にする．この表現に込められた意味や気持ちはわからないわけでもないが，数学的には正しくない．負けの可能性はなく，必ず勝つというならば「今夜は確率1で勝つ」というのが正しい言い方である．

例題　2つのさいころA,Bを同時に投げたとき，次の確率を求めよ．
(1) 出た目の和が4になる．
(2) 出た目の積が奇数になる．

答

　さいころA，Bの出た目をそれぞれ $a,\ b$ として根元事象を$(a, b)$ で表すと，1回の試行によって起こり得るすべての場合は次の36通りで，これらは同様に確からしい．

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

(1)　

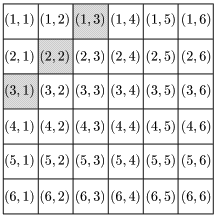
和が4になるのは

(1,3), (2,2), (3,1)

の3通りであるから求める確率は，

$$\frac3{36}=\underline{\boldsymbol{\frac1{12}}}$$

(2)　

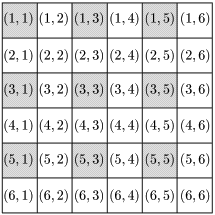
　積が奇数になるのは $a, b$ がともに奇数となるときで，図の網掛け部分の9通りがあるから，求める確率は，

$$\frac9{36}=\underline{\boldsymbol{\frac14}}$$

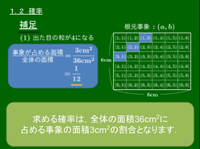
重要な補足　[確率と面積の関係]

　確率は面積と関連付けておくと理解しやすい上に，実はこの考え方こそ確率論の本質でもある．例えばこの例題の場合，全事象を1辺の長さが 6cm の正方形の面積と考える：

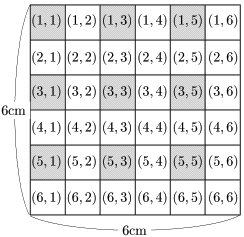
　「同様に確からしい」というのは根元事象の面積が等しい(ここではどれも $1{\rm cm}^2$ )ということである．

　この考え方で例題の(1)を考えると，確率は

$$\frac{\mbox{事象が占める面積}}{\mbox{全体の面積}}=\frac{3{\rm cm}^2}{36{\rm cm}^2}=\frac1{12}$$

となる．

---

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率	[無料]
2. 確率の基本性質	[無料]
3. 独立な試行の確率	[会員]
4. 反復試行の確率	[会員]
5. 条件付き確率	[会員]