19．パラメータが2次で表された直線の通過領域

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

19.1 はじめに

　入試問題を解いていると，東京大学や京都大学を始め，多くの大学で2次方程式の解の配置問題が出題されていると気が付きます．例えば次のような問題です．

　この問題は，$L:y=2x\ (0\leqq x\leqq1)$ と表されますから，曲線 $y=x^2+ax+b$ が $L$ と共有点をもつための条件は，2次方程式 $x^2+ax+b=2x$ 即ち $$x^2+(a-2)x+b=0$$ が，$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことです．これを2次方程式の解の配置問題として解く方法の他に，ファクシミリの原理 を利用した解法もありますが，第3の解法として，図形の通過領域として捉える考え方があります．教科書で説明されることはまずないと思われるこの解法を，以下で詳しく見ていきます．

19.2 包絡線とは

　以下で扱う題材は直線で，しかもパラメータが2次で表された直線です．この文脈で最も利用される直線を例にとりましょう．

例：$y=2tx-t^2$

　これはパラメータ $t$ の2次式で表された直線です．このようにパラメータが2次で表されたものに限定して議論を進めますが，パラメータが２次であれば，実は直線でなくても曲線でも成り立ちます．例えば高校数学ワンポイント1. ファクシミリの原理 の東京大学の過去問(ページ最下部)を参照してください．また，難関大の入試問題の多くはこのパターンだけで用が足ります．

　この直線は，$t$ を決めると直線が1つ決まります．$t$ のいくつかの値での直線は次のようになります．

　$t=-2$ のとき　$y=-4x-4$
　$t=-1$ のとき　$y=-2x-1$
　$t=0$ のとき　$y=0$
　$t=1$ のとき　$y=2x-1$
　$t=2$ のとき　$y=4x-4$

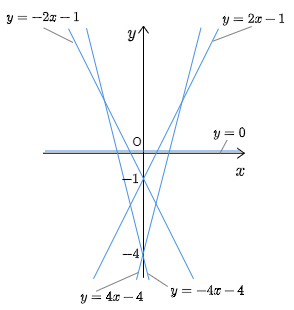
　そして次が重要なのですが，これらの直線はある1つの曲線に接しているのです．

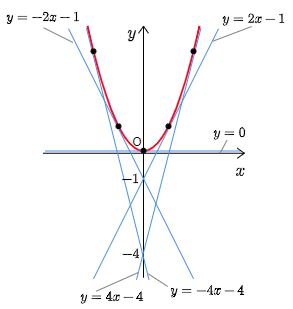
　この赤色の曲線は，放物線 $y=x^2$ です．今，5つの $t$ の値について見ましたが，実は任意の実数 $t$ について調べると，もれなくその直線はこの放物線の接線となっているのです．このとき，この放物線 $y=x^2$ をこの直線群の包絡線(ほうらくせん，envelope)といいます．

包絡線とは　直線群の1本1本が，常にある曲線 $C$ の接線になっているとき，この曲線 $C$ をその直線群の包絡線という．

　この包絡線さえわかれば，パラメータに伴って変化する直線の動きを目で捕捉することが可能となり，直線の通過領域に関する問題は一気に答えまでたどり着くことが可能となります．

19.3 包絡線の求め方

　ではどのようにすれば包絡線が求められるのでしょうか．大学の教科書を参照すると，概ね次のように書かれています．

包絡線の求め方　直線群 $F(x,\ y,\ t)=0$ に対して，2つの式
　　　$F(x,\ y,\ t)=0$ …①
　　　$F_t(x,\ y,\ t)=0$ …②
から $t$ を消去して得られる曲線 $C$ は，この直線群の包絡線である．

　順に説明していきます．

　まず，①式の $F(x,\ y,\ t)=0$ というのは，先の例でいうと $y=2tx-t^2$ のことです．この式は $2tx-y-t^2=0$ と書き換えることができますから，$F(x,\ y,\ t)$ というのは $2tx-y-t^2$ を指しています．

　次に，②式の $F_t(x,\ y,\ t)=0$ ですが，左辺の $F_t(x,\ y,\ t)$ というのは $F$ の添え字である $t$ 以外は定数と思って文字 $t$ について微分せよという意味です．先の例でいうと，$F(x,\ y,\ t)=2tx-y-t^2$ において $x$ と $y$ は定数だと思って $t$ で微分すると，

$$F_t(x,\ y,\ t)=2x-2t$$

となります．これが０となるとき，$2x-2t=0$，つまり $t=x$ です．

　この関係を①に代入すると，包絡線がわかるというのが定理の主張です．実際に代入してみると

$$2x\cdot x-y-x^2=0\ \ \therefore y=x^2$$

となって，確かに包絡線が放物線 $y=x^2$ であることがわかりました．

　では何故このようにすれば包絡線が求められるのでしょうか．気になるところではありますが，証明については思い切って省略したいと思います．とにかくこの定理を認めて，大学入試の記述で使えるような範囲で利用していきたいというのが目的です．

19.4 パラメータが2次で表された直線の包絡線の求め方

　本稿では，直線群をパラメータが2次で表された直線に限定していましたが，このタイプの直線は次のように平方完成というごく身近な道具を使って包絡線を求めることができるのです．先の例を使って説明していきましょう．

　直線 $y=2tx-t^2$ を $t$ について整理すると

$$t^2-2tx+y=0$$

　左辺を $t$ の2次関数と見て平方完成すると

$$(t-x)^2+\underline{y-x^2}_{\mbox{①}}=0$$

　このとき，平方式を除いた下線部①$=0$ が，包絡線の方程式となっています．実際直線の式 $(t-x)^2+y-x^2=0$ と $y-x^2=0$ を連立すると $(x-t)^2=0$ となりますから，直線と放物線は $x=t$ で接することがわかります．

　こういったことがパラメータが2次で表された直線(曲線)であるときに常にいえることなのです．冒頭の京都大学の入試問題をこの方針で解いてみましょう．

解答例

　$L:y=2x\ (0\leqq x\leqq1)$ と表されるから，曲線 $y=x^2+ax+b$ が $L$ と共有点をもつための条件は，2次方程式 $x^2+ax+b=2x$ 即ち
$$x^2+(a-2)x+b=0$$
が，$0\leqq x\leqq1$ の範囲に少なくとも1つの解をもつことである．$x=t\ (0\leqq t\leqq1)$ のとき，$a,\ b$ が満たすべき条件は $t^2+(a-2)t+b=0$ すなわち $b=-ta-t^2+2t$ (…①) で，これは $ab$ 平面上において直線を表す．

【メモ】
　ここで計算用紙に，平方完成によって包絡線を先に計算しておきます．
　$t^2+(a-2)t+b=0$
　→ $\left(t+\dfrac{a-2}2\right)^2+\underline{b-\dfrac{(a-2)^2}4}=0$
　よって$ab$ 平面上における包絡線の方程式は
　　$b-\dfrac{(a-2)^2}4=0$，つまり $b=\dfrac{(a-2)^2}4$

(実際の記述ではここから包絡線云々は書かないで，発見的に包絡線を見つけてきたというていで)

　ここで，$ab$ 平面上の放物線 $b=\dfrac{(a-2)^2}4$ を考えると，これは先の直線①と接する．実際 $b$ を消去して整理すると

$$\dfrac{(a-2)^2}4=-ta-t^2+2t$$ $$a^2+4(t-1)a+\{2(t-1)\}^2=0$$ $$(a+2t-2)^2=0$$

となるから，直線①と放物線 $b=\dfrac{(a-2)^2}4$ は $a=-2t+2$ で接する．いま $0\leqq t\leqq1$ で $t$ を動かすと，$0\leqq a\leqq 2$ となるから，直線①をこの範囲で放物線 $b=\dfrac{(a-2)^2}4$ と接するように動かしたときの通過領域は，次図の境界線を含む斜線領域となる．そしてこれが求める実数の組 $(a,\ b)$ の集合である．

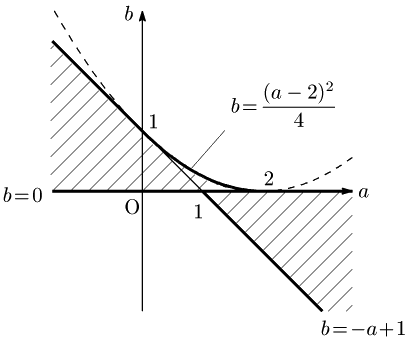
19.5 なぜ平方完成で包絡線がわかるか

　最後に，パラメータが2次で表された直線(曲線)の場合にどうして平方完成すると包絡線がわかるかを確認しておきます．包絡線の求め方は次のようでした．