18．f(f(x))=x の形をした関数方程式の取り扱い方

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理	[会員]
2. バウムクーヘン分割	[会員]
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

18.1 ちょっと不思議な形の方程式

　次の例題を考えてみてください。

例題1　$(x^2-6)^2-6=x$ を解け．

こたえ

　与式の左辺を展開して整理します．

$$(x^4-12x^2+36)-6=x$$

$x^4-12x^2-x+30=0$　…①

　この方程式①の左辺に $x$ に3を代入すると

$$3^4-12\cdot3^2-3+30=81-108-3+30=0$$

　また $x=-2$ を代入しても

$$(-2)^4-12\cdot(-2)^2-(-2)+30=16-48+2+30=0$$

　従って因数定理 により，方程式①の左辺は $(x-3)(x+2)$ を因数にもちますから，実際に割り算を行うと

① $\iff (x-3)(x+2)(x^2+x-5)=0$

となります．よって残りの解は $x^2+x-5=0$ を解いて，$x=\dfrac{-1\pm\sqrt{21}}2$ となります．

　答えは　$x=3,\ -2,\ \dfrac{-1\pm\sqrt{21}}2$

例題2　$6(6x^2-2)^2-2=x$ を解け．

こたえ

　与式の左辺を展開して整理します．

$$6(36x^4-24x^2+4)-2=x$$

$216x^4-144x^2-x+22=0$　…②

　この方程式②の左辺に $x$ に $-\dfrac12$ を代入すると

$$\begin{align*} &216\cdot\left(-\dfrac12\right)^4-144\cdot\left(-\dfrac12\right)^2-\left(-\dfrac12\right)+22\\ =&\dfrac{27}2-36+\dfrac12+22=0 \end{align*}$$

　また $x=\dfrac23$ を代入しても

$$\begin{align*} &216\cdot\left(\dfrac23\right)^4-144\cdot\left(\dfrac23\right)^2-\dfrac23+22\\ =&\dfrac{128}3-64-\dfrac23+22=0 \end{align*}$$

　従って因数定理 により，方程式②の左辺は $(2x+1)(3x-2)$ を因数にもちますから，実際に割り算を行うと

② $\iff (2x+1)(3x-2)(36x^2+6x-11)=0$

となります．よって残りの解は $36x^2+6x-11=0$ を解いて，$x=\dfrac{-1\pm3\sqrt5}{12}$ となります．

　答えは　$x=-\dfrac12,\ \dfrac23,\ \dfrac{-1\pm3\sqrt5}{12}$

　いかがでしたか？かなり難しいと感じられた方が多いのではないでしょうか．とりわけ例題2で発見的に $-\dfrac12$ や $\dfrac23$ を見つけてくるのは容易ではありません．難しいのは当然です．

　しかし実は，例題1では方程式①の左辺が $(x+3)(x-2)$，すなわち $x^2-x-6$ を因数にもつことが出発の最初からわかっていました．例題2でも同様で，問題を読んだ瞬間から方程式②の左辺が $(2x+1)(3x-2)$，すなわち $6x^2-x-2$ を因数にもつことがわかっていたのです．どうしてそんなことがわかっていたのでしょうか．

18.2 $f(f(x))=x$ の取り扱い方

　これら2つの例題を慎重に眺めていると，とてもよく似た形をしていることに気が付きます．もう一度2つの例題をじっくり見てみましょう．

例題1：$(x^2-6)^2-6=x$
例題2：$6(6x^2-2)^2-2=x$

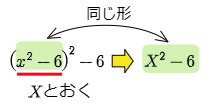
　例題1ではカッコの中身である $x^2-6$ を $X$ とおくと，左辺は $X^2-6$ となって，$X$ とおいた式と全く同じ形になっています．

　同様に，例題2でもカッコの中身である $6x^2-2$ を $X$ とおくと，左辺は $6X^2-2$ となって， $X$ とおいた式と全く同じ形になっています．これを言い換えると，例題1では $f(x)=x^2-6$ とおくと，左辺は $f(f(x))$ と表せます．

※　$f(f(x))$ の表現がわかりにくい場合は，$f(X)=X^2-6$ の $X$ のところに $f(x)$ を代入したと捉えてください．$f(x)=x^2-6$ ですから，左側の $X$ には $f(x)$ を，右側の $X$ には $x^2-6$ を代入します．すると $f(f(x))$ が $(x^2-6)^2-6$ を表していることがわかります．

　例題2でも同様です．$f(x)=6x^2-2$ とおくと，左辺は $f(f(x))$ と表せます．つまりこの2つの例題の共通点は，

方程式 $f(f(x))=x$ を解く

ということなのです．このように関数を含んだ方程式を関数方程式といいます．いま右辺の $x$ を左辺に移項して $f(f(x))-x=0$ としておきましょう．このタイプの関数方程式の取り扱い方は

方程式 $f(f(x))-x=0$ は，
方程式 $f(x)-x=0$ の解をすべて含む

すなわち

ポイント$f(f(x))-x$ は$f(x)-x$ を因数にもつ

ということに注目して因数分解を行うというのが定石です．