14．3次関数のグラフの特徴【ノート】
1人で学べる！高校数学

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理
2. バウムクーヘン分割
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル

13．3次関数のグラフの特徴

　3次関数のグラフの特徴を紹介します．最大・最小問題を考える際，しばしば極大値や極小値と同じ値をとる $x$ の値が必要になりますが，そういった際にここで書かれたグラフの特徴を知っていると，とりわけ共通テストなどで大幅な時間短縮が図れます．

特徴1．グラフは点対称

　3次関数 $f(x)=a{x}^3+b{x}^2+cx+d$ について，$y=f(x)$ のグラフを $x$軸方向に ${\displaystyle \frac{b}{3a}}$，$y$ 軸方向に $-f(-{\displaystyle \frac{b}{3a}})$ だけ平行移動したグラフの方程式は

$$\begin{array}{rl}y+f(-\frac{b}{3a})=a{(x-\frac{b}{3a})}^3+b{(x-\frac{b}{3a})}^2+c& (x-\frac{b}{3a})+d\\ & \cdots \text{①}\end{array}$$

です．ここで，

$$\begin{array}{rl}f(-\frac{b}{3a})& =a{(-\frac{b}{3a})}^3+b{(-\frac{b}{3a})}^2+c(-\frac{b}{3a})+d\\ & =-\frac{b^3}{27a^2}+\frac{b^3}{9a^2}-\frac{bc}{3a}+d\\ a{(x-\frac{b}{3a})}^3& =a(x^3-\frac{b}{a}{x}^2+\frac{b^2}{3a^2}x-\frac{b^3}{27a^3})\\ & =a{x}^3-b{x}^2+\frac{b^2}{3a}x-\frac{b^3}{27a^2}\\ b{(x-\frac{b}{3a})}^2& =b(x^2-\frac{2b}{3a}x+\frac{b^2}{9a^2})\\ & =b{x}^2-\frac{2b^2}{3a}x+\frac{b^3}{9a^2}\\ c(x-\frac{b}{3a})& =cx-\frac{bc}{3a}\end{array}$$

となりますから①式は，

$$y=a{x}^3+(c-\frac{b^2}{3a})x$$

となります．この右辺を $g(x)$ とおくと，任意の $x$ に対して

$$g(-x)=-g(x)$$

が成り立ちますから $g(x)$ は奇関数です．奇関数のグラフは原点に関して対称です．従って一般に3次関数のグラフについて次が成り立ちます：

　対称の中心は，グラフの凸性が変化する点で，この点を変曲点といいます．詳しくは数学Ⅲ 11.関数のグラフ を参照してください．

特徴2．グラフの箱詰め

　一般にグラフを平行移動しただけではそのグラフの形は変化しません．特徴1. で見たように，どんな3次関数のグラフも変曲点に関して対称であり，変曲点が原点にくるように平行移動すると，そのグラフをもつ関数は奇関数ですから，今後グラフの特徴を考察するに当たっては $y=a{x}^3+bx$ という形の3次関数を考えるので十分です．

　さて，$f(x)=a{x}^3+bx$ とおき，$f(x)$ が $x=\alpha$ で極値 $f(\alpha )$をとるとします．$f(\alpha )=k$ とすると，$f(x)=k$ となる $x$ は，$\alpha$ 以外にもう1つ存在します．それを $p$ とします：

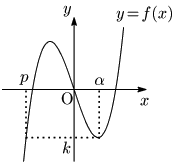
　$p$ は3次方程式 $a{x}^3+bx=k$，即ち

$$a{x}^3+bx-k=0$$

の解です．$\alpha$ がこの方程式の重解であることに注意をすれば，3次方程式の解と係数の関係により

$$\alpha +\alpha +p=0$$

$$\therefore p=-2\alpha$$

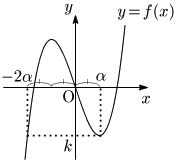
　3次関数のグラフの対称性により，$f(x)=-k$ となる $-\alpha$ 以外の $x$ の値は $2\alpha$ です．従ってグラフは次のようになります：

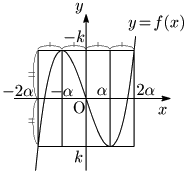
　このように3次関数のグラフは箱詰めして考えると捉えやすくなります．

　3次関数の最大・最小を考える際，しばしば極大値や極小値と同じ値をとる別の $x$ の値が必要となりますが，そのときにこの事実は絶大な効果を発揮します．

特徴②　3次関数のグラフは長方形領域に箱詰めすると，等間隔に様々な値が得られる．

高校数学[総目次]

高校数学ワンポイント

	スライド	ノート
1. ファクシミリの原理
2. バウムクーヘン分割
3. 円と放物線
4. 垂線の長さ
5. 不定方程式
6. 関数の連続性は導関数に遺伝するか
7. 極方程式における $r$ の正負について
8. 極座標表示における扇形分割積分
9. 素因数分解の一意性
10. 三角関数の不定積分
11. コーシー・シュワルツの不等式
12. 放物線と2接線で囲まれた部分の面積
13. 整式の除法(発展編)
14. 3次関数のグラフの特徴
15. 曲線の長さを求める公式の証明について
16. もう迷わない！必要条件・十分条件のくすっと笑える判定方法
17. 同じものを含む円順列の考え方
18. $f(f(x))=x$ の形をした関数方程式の取り扱い方
19. パラメータが2次で表された直線の通過領域
20. 四面体の面上及び内部を表すベクトル