軸まわりの回転体の体積を計算する際に,強力な威力を発揮するのが「バウムクーヘン分割」という考え方をする積分法です.バウムクーヘン分割という言葉は東京出版の書籍で用いられ始めた印象的な用語です.例を用いて教科書的な考え方とバウムクーヘン分割を用いた考え方の2つを示します.
また,何故そのような考え方で体積が計算できるのかの証明も行います.
最後に,教科書的な考え方とバウムクーヘン分割との関係を説明します.
高校数学(総目次)
高校数学ワンポイント
| スライド | ノート | |
| 1. ファクシミリの原理 | [会員] | |
| 2. バウムクーヘン分割 | [会員] | |
| 3. 円と放物線 | ||
| 4. 垂線の長さ | ||
| 5. 不定方程式 | ||
| 6. 関数の連続性は導関数に遺伝するか | ||
| 7. 極方程式における の正負について | ||
| 8. 極座標表示における扇形分割積分 | ||
| 9. 素因数分解の一意性 | ||
| 10. 三角関数の不定積分 | ||
| 11. コーシー・シュワルツの不等式 | ||
| 12. 放物線と2接線で囲まれた部分の面積 | ||
| 13. 整式の除法(発展編) | ||
| 14. 3次関数のグラフの特徴 | ||
| 15. 曲線の長さを求める公式の証明について | ||
| 16. もう迷わない!必要条件・十分条件のくすっと笑える判定方法 | ||
| 17. 同じものを含む円順列の考え方 | ||
| 18. の形をした関数方程式の取り扱い方 | ||
| 19. パラメータが2次で表された直線の通過領域 | ||
| 20. 四面体の面上及び内部を表すベクトル |

2.バウムクーヘン分割
スライドはぜひ全画面表示で
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
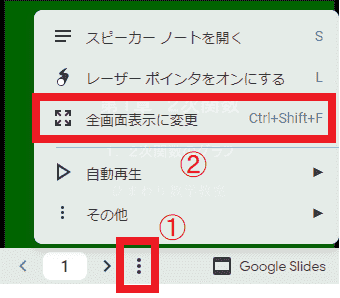
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
