4. 無限等比級数(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第1章　極限

	スライド	ノート	問題
1. 数列の極限	[無料]
2. 無限等比数列	[無料]
3. 無限級数	[会員]		[会員]
4. 無限等比級数	[会員]
5. 関数の極限	[会員]
6. (sin x)/x の極限	[会員]
7. 関数の連続性	[会員]

4.1 無限等比級数の収束と発散

$$a+ar+ar^2+\cdots+ar^{n-1}+\cdots \ \cdots \mbox{①}$$ を初項 $a$，公比 $r$ の無限等比級数という．

　①の第 $n$ 項までの部分和を $S_n$ とし，無限等比級数 $\displaystyle\sum_{n=1}^\infty ar^{n-1}=\lim_{n\to\infty}S_n$ を調べる．

$\underline{a=0\ \mbox{のとき}}$ $$S_n=0+0+\cdots+0=0\ \to\ 0\ (n\to\infty)$$ $\underline{a\neq0\ \mbox{のとき}}$
　i) $|r|<1$ のとき
　　　$S_n=\dfrac{a(1-r^n)}{1-r}\to\dfrac a{1-r}\ (n\to\infty)$
　　　よって，数列$\{S_n\}$ は収束．
　ii) $r=1$ のとき
$$S_n=a+a+\cdots +a=na.$$ 　　よって，$n\to\infty$ のとき，$\{S_n\}$ は発散．
　iii) $r\leqq -1,\ 1<r$ のとき
　　　$S_n=\dfrac{a(1-r^n)}{1-r}$ で，$r^n$ が発散するから $\{S_n\}$ は発散．

まとめ 　無限等比級数$\displaystyle\sum_{n=1}^\infty ar^{n-1}=a+ar+ar^2+\cdots$（ただし，$a\neq 0$）は
　　$|r|<1$ のとき収束して，和は $\dfrac a{1-r}$．
　　$|r|\geqq 1$ のとき，発散．

4.2 無限等比級数と循環小数

Q.　$0.1\dot{2}\dot{3}=0.1232323\cdots$ を分数で表すと？
A.　 $$\begin{align*} 0.1\dot{2}\dot{3}&=0.1+0.023+0.00023+0.0000023+\cdots\\ &=\frac 1{10}+\underline{\frac{23}{10^3}+\frac{23}{10^5}+\frac{23}{10^7}+\cdots}\\ &=\frac 1{10}+\frac{\frac{23}{10^3}}{1-\frac 1{10^2}}\\ &=\frac 1{10}+\frac{23}{990}=\frac {122}{990}=\frac{61}{495} \end{align*}$$ ※下線部分が，初項 $\dfrac{23}{10^3}$，公比 $\dfrac 1{10^2}$ の無限等比級数になっている．

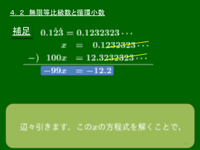
補足

$$\begin{array}{rl} x&=\ \ 0.1232323\cdots\\ -)\ \ 100x&=12.3232323\cdots\\ \hline -99x&=-12.2 \end{array}$$ $$\therefore\ x=\frac{12.2}{99}=\frac{61}{495}.$$

---

高校数学[総目次]

数学Ⅲ　第1章　極限

	スライド	ノート	問題
1. 数列の極限	[無料]
2. 無限等比数列	[無料]
3. 無限級数	[会員]		[会員]
4. 無限等比級数	[会員]
5. 関数の極限	[会員]
6. (sin x)/x の極限	[会員]
7. 関数の連続性	[会員]