4. 定積分とその性質(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]		[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ

4．定積分とその性質

4.1 定積分とは

　定積分については既に数学Ⅱで学習済みである．しかしここまでの学習で，積分できる関数のクラスは数学Ⅱまでの範囲とは比較にならないほど広がった．そこで改めて定積分とは何なのかという復習から始めたい．

定積分とは　閉区間 $[a,b]$ で連続な関数 $f(x)$ の不定積分(原始関数)を $F(x)$ とすれば， $$F(b)-F(a)\ \ \cdots\mbox{①}$$ を「関数 $f(x)$ の $a$ から $b$ までの定積分」といい，①を $$\int_a^b\!f(x)\,dx$$ で表す．

　定義の中に $f(x)$ の連続性があるが，これは積分可能性に関する断り書きであって，高校数学の範囲ではこの点が問題になることはほとんどない．数学Ⅱの定積分 の説明ではこのような記載はなかったが，それは数学Ⅱの定積分で相手にする関数が整式に限られていたためである．整式とは $2x+3$ や $x^2$ などのことを指すが，これらは実数全体で連続だから，もちろんその一部である閉区間 $[a, b]$ でも連続である．

補足1

　①は $\Bigl[F(x)\Bigr]_a^b$ とも表す．即ち

$$\int_a^bf(x)dx=\Bigl[F(x)\Bigr]_a^b=F(b)-F(a)$$

補足2

　$F(x)+C\ (C$ は定数)もまた $f(x)$ の不定積分であるが， $$\begin{align*} \Bigl[F(x)+C\Bigr]_a^b&=\{F(b)+C\}-\{F(a)+C\}\\[5pt] &=F(b)-F(a) \end{align*}$$ であるから定積分の値は変わらない．

補足3

　定数 $a,b$ に対して①は(定数)$-$(定数)だから，定積分は定数である．( $x$ の関数ではない．)

4.2　定積分の性質

$$\begin{align*} &\mbox{①}\ \int_a^b\!kf(x)\,dx=k\int_a^b\!f(x)\,dx\ \ (k\ \mbox{は定数})\\[5pt] &\mbox{②}\ \int_a^b\!\{f(x)\!+\!g(x)\}dx=\int_a^b\!f(x)\,dx\!+\!\int_a^b\!g(x)\,dx\\[5pt] &\mbox{③}\ \int_a^b\!f(x)\,dx=-\int_b^a\!f(x)\,dx\\[5pt] &\hspace{5mm}\left(\mbox{特に，}\int_a^a\!f(x)\,dx=0\right)\\[5pt] &\mbox{④}\ \int_a^b\!f(x)\,dx=\int_a^c\!f(x)\,dx+\int_c^bf(x)\,dx \end{align*}$$

証明

③ $$\begin{align*} \mbox{左辺}&=F(b)-F(a)\\[5pt] &=-\{F(a)-F(b)\}\\[5pt] &=\mbox{右辺} \end{align*}$$ 　また，③において $b$ も $a$ とおくと， $$\int_a^a\!\!f(x)\,dx=-\int_a^a\!\!f(x)\,dx$$ $$\therefore \int_a^a\!\!f(x)\,dx=0$$ 　(定義より $\displaystyle\int_a^a\!\!f(x)\,dx\!=\!F(a)\!-\!F(a)=0$ でもよい．)

④ $$\begin{align*} \mbox{右辺}&=\{F(c)-F(a)\}+\{F(b)-F(c)\}\\[5pt] &=F(b)-F(a)\\[5pt] &=\mbox{左辺} \end{align*}$$

■

4.3　絶対値のついた関数の定積分

例題　定積分 $\displaystyle\int_{-1}^2|x^2-4x|dx$ を求めよ．

　被積分関数に絶対値が含まれる場合，そのままの状態で積分しようとしてはいけない．積分する際は，常に絶対値記号を外してから行うのである．絶対値記号を外すといっても，定義域全体を考える必要はない．私たちが関心があるのは積分区間である $[-1,\ 2]$ だけである．この区間内で，絶対値記号の中身が0以上か否かを判定する．そして，積分区間の途中で符号が変わるたびに，積分区間を分けて計算しなければならない．

ポイント
　絶対値のついたままでは積分できない

こたえ

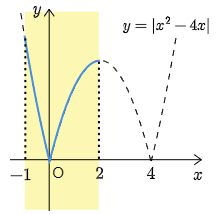
　積分区間である $[-1,\ 2]$ において，

$$|x^2-4x|=\left\{\begin{array}{ll}x^2-4x&(-1\leqq x\leqq0)\\[5pt]-(x^2-4x)&(0\leqq x\leqq2)\end{array}\right.$$

　よって

$$\begin{align*} \int_{-1}^2|x^2-4x|dx&=\int_{-1}^0(x^2-4x)dx+\int_0^2\{-(x^2-4x)\}dx\\[5pt] &=\left[\frac{x^3}3-2x^2\right]_{-1}^0-\left[\frac{x^3}3-2x^2\right]_0^2\\[5pt] &=\frac{0^3-(-1)^3}3-2\{0^2-(-1)^2\}-\left\{\frac{2^3-0^3}3-2(2^2-0^2)\right\}\\[5pt] &=\dfrac13+2-\left(\frac83-8\right)\\[5pt] &=\frac{23}3 \end{align*}$$

補足

　絶対値を含む関数の積分では，符号違いの同じ関数を積分することがしばしばである．本問においても，$x^2-4x$ と $-(x^2-4x)$ は符号が異なるだけである．こういった場合の積分計算では同じ式を何度も書くことになり，見た目が見にくい上に書くのも疲れる．そこで次のように予め原始関数を計算しておくと，見やすくなる上に記述が簡略化できる．

こたえ(その2)

　$f(x)=x^2-4x$，$F(x)=\dfrac{x^3}3-2x^2$ とおく．(←ここがポイント)

　積分区間である $[-1,\ 2]$ において，

$$|x^2-4x|=\left\{\begin{array}{ll}x^2-4x&(-1\leqq x\leqq0)\\[5pt]-(x^2-4x)&(0\leqq x\leqq2)\end{array}\right.$$

であるから，

$$\begin{align*} \int_{-1}^2|x^2-4x|dx&=\int_{-1}^0f(x)dx+\int_0^2\{-f(x)\}dx\\[5pt] &=\Bigl[F(x)\Bigr]_{-1}^0-\Bigl[F(x)\Bigr]_0^2\\[5pt] &=2F(0)-F(-1)-F(2)\\[5pt] &=2\cdot0-\left(-\dfrac13-2\right)-\left(\frac83-8\right)\\[5pt] &=\frac{23}3 \end{align*}$$

---

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]		[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ