13. 曲線の長さ

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]		[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ

13．曲線の長さ

13.1 媒介変数表示された曲線の長さ

　曲線が，媒介変数 $t$ を用いて

$$\left\{ \begin{array}{l} x=f(t)\\[5pt] y=g(t)\end{array}\right.\ \ \ (\alpha\leqq t\leqq\beta)$$

で表されているとする．ただし，$f(t),\ g(t)$ の導関数は連続とする．

　この曲線の長さ $L$ は次で表される：

曲線の長さ $$\begin{align*} L&=\int_\alpha^\beta\!\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt\\[5pt] &=\int_\alpha^\beta\!\sqrt{\{f'(t)\}^2+\{g'(t)\}^2}\,dt \end{align*}$$

説明

　点AからPまでの曲線の長さを $s(t)$ とすると，$s(t)$ は $t$ の増加関数である．$t$ の増分 $\Delta t$ に対する $s$，$x$，$y$ の増分をそれぞれ $\Delta s$，$\Delta x$，$\Delta y$，とすると，三平方の定理により

$$\Delta s\fallingdotseq\sqrt{(\Delta x)^2+(\Delta y)^2}$$

　$\Delta s$ と $\Delta t$ は同符号だから，

$\dfrac{\Delta s}{\Delta t}\fallingdotseq\sqrt{\left(\dfrac{\Delta x}{\Delta t}\right)^2+\left(\dfrac{\Delta y}{\Delta t}\right)^2}$　　$\cdots$ ①

　ここで，$\Delta t\to 0$ とすると，

$$\begin{align*} \lim_{\Delta t\to 0}\frac{\Delta s}{\Delta t}&=\lim_{\Delta t\to 0}\frac{s(t+\Delta t)-s(t)}{\Delta t}=\frac{ds}{dt}\Bigl(=s'(t)\Bigr)\\[5pt] \lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}&=\lim_{\Delta t\to 0}\frac{f(t+\Delta t)-f(t)}{\Delta t}=\frac{dx}{dt}\Bigl(=f'(t)\Bigr)\\[5pt] \lim_{\Delta t\to 0}\frac{\Delta y}{\Delta t}&=\lim_{\Delta t\to 0}\frac{g(t+\Delta t)-g(t)}{\Delta t}=\frac{dy}{dt}\Bigl(=g'(t)\Bigr) \end{align*}$$

であり，このとき①の両辺の差は0に近付く^* (下の注参照)から，

$$\frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}$$

即ち

$\therefore s'(t)=\sqrt{\{f'(t)\}^2+\{g'(t)\}^2}$

となる．

(注)　この部分の詳細な議論はこちら．

　この式の両辺を $\alpha$ から $\beta$ まで積分して

$\displaystyle\int_\alpha^\beta s'(t)\,dt=\int_\alpha^\beta\!\sqrt{\{f'(t)\}^2+\{g'(t)\}^2}\,dt\ \ \cdots$ ②

を得る．左辺は，

$$\begin{align*} \int_\alpha^\beta s'(t)\,dt&= \Bigl[s(t)\Bigr]_\alpha^\beta\\[5pt] &=s(\beta)-s(\alpha) \end{align*}$$

となり，$s(t)$ の定義から $s(\alpha)=0$，そして $s(\beta)=L$ であるから，②は

$$L=\int_\alpha^\beta\!\sqrt{\{f'(t)\}^2+\{g'(t)\}^2}\,dt$$

■

例題　$a>0$ とする．次のサイクロイド曲線の長さ $L$ を求めよ． $$\left\{\begin{array}{l} x=a(t-\sin t)\\[5pt] y=a(1-\cos t) \end{array}\right.\ \ \ (0\leqq t\leqq 2\pi)$$

こたえ

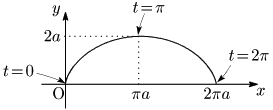
　$\dfrac{dx}{dt}=a(1-\cos t)$，$\dfrac{dy}{dt}=a\sin t$ により，

$$\begin{align*} \left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2&=a^2\{(1-\cos t)^2+\sin^2t\}\\[5pt] &=2a^2(1-\cos t)\\[5pt] &=4a^2\cdot\frac{1-\cos t}2\\[5pt] &=4a^2\sin^2\frac t2 \end{align*}$$

　よって，

$$\begin{align*} \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}&=\sqrt{4a^2\sin^2\frac t2}\\[5pt] &=2a\left|\sin\frac t2\right|\\[5pt] &=2a\sin\frac t2\ \ (\because 0\leqq\frac t2\leqq\pi) \end{align*}$$

となるから，

$$\begin{align*} L&=\int_0^{2\pi}2a\sin\frac t2\,dt\\[5pt] &=\left[-4a\cos\frac t2 \right]_0^{2\pi}\\[5pt] &=-4a(\cos\pi-\cos 0)\\[5pt] &=\underline{{\boldsymbol 8a}} \end{align*}$$

13.2 $y\!=\!f(x)$ で表された曲線の長さ

　曲線 $y=f(x)\ (a\leqq x\leqq b)$ のとき，

$$\left\{\begin{array}{l}x=t\\[5pt] y=f(t) \end{array}\right.\ \ (a\leqq t\leqq b)$$

と考えると，

$$\frac{dx}{dt}=1,\ \ \frac{dy}{dt}=f'(t)$$

であるから，この曲線の長さ $L$ は

$$L=\int_a^b\sqrt{1+{f'(t)}^2}\,dt$$

　$t$ を $x$ に置き換えて次を得る：

　曲線 $y=f(x)\ (a\leqq x\leqq b)$ の長さ $L$ は $$L=\int_a^b\sqrt{1+\{f'(x)\}^2}\,dx$$

補足

　この形では，弧長が簡単に求まるものは少ない．入試によく出るのは，$ax^{\frac32}$ や$\displaystyle\frac{e^x+e^{-x}}2$ (カテナリー)など．

例題　曲線 $y=\dfrac12(e^x+e^{-x})$ $(0\leqq x\leqq 1)$ の長さを求めよ．

こたえ

　$y’=\dfrac12(e^x-e^{-x})$ により，

$$\begin{align*} 1+{y’}^2&=1+\frac14(e^{2x}-2+e^{-2x})\\[5pt] &=\frac14(e^{2x}+2+e^{-2x})\\[5pt] &=\left\{\frac12(e^x+e^{-x})\right\}^2 \end{align*}$$

　故に，

$$\sqrt{1+{y’}^2}=\frac12|e^x+e^{-x}|=\frac12(e^x+e^{-x})$$

　よって，

$$\begin{align*} L&=\int_0^1\frac12(e^x+e^{-x})\,dx\\[5pt] &=\left[\frac12(e^x-e^{-x})\right]_0^1\\[5pt] &=\frac12\{(e-e^{-1})-(1-1)\}\\[5pt] &=\underline{\boldsymbol{\frac12\left(e-\frac1e\right) }} \end{align*}$$

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質	[会員]
5. 置換積分法（定積分）	[会員]
6. 部分積分法（定積分）	[会員]
7. 定積分と微分法	[会員]
8. 定積分と和の極限	[会員]
9. 定積分と不等式	[会員]
10. 定積分の応用（面積）	[会員]
11. 定積分の応用（体積）	[会員]		[会員]
12. 定積分の応用（回転体の体積）	[会員]
13. 曲線の長さ