高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | [会員] | ||
| 5. 置換積分法(定積分) | [会員] | ||
| 6. 部分積分法(定積分) | [会員] | ||
| 7. 定積分と微分法 | [会員] | ||
| 8. 定積分と和の極限 | [会員] | ||
| 9. 定積分と不等式 | [会員] | ||
| 10. 定積分の応用(面積) | [会員] | ||
| 11. 定積分の応用(体積) | [会員] | [会員] | |
| 12. 定積分の応用(回転体の体積) | [会員] | ||
| 13. 曲線の長さ |

10.定積分の応用(面積)
10.1 面積
関数 y=f(x) が区間 [a, b] で常に0以下の値をとるとする.このとき定積分 ∫baf(x)dx の値は,y=f(x) のグラフと x 軸,及び2直線 x=a,x=b とで囲まれた部分の面積を S とすれば,数学Ⅱの積分法のところで学んだように −S となるのであった.
∫baf(x)dx=−S
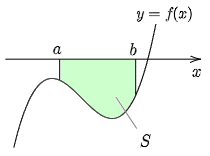
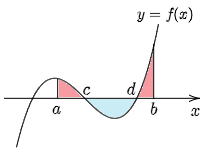
一般には関数 y=f(x) は,区間 [a, b] で正の値をとったり負の値をとったりすることがあるため,x 軸,及び2直線 x=a,x=b とで囲まれた部分の面積が知りたい場合は,符号が入れ替わるごとに積分区間を分けて計算しなければならない.例えば,y=f(x) のグラフが下の図1のような場合,赤色と青色の面積の合計を T とすると
T=∫caf(x)dx−∫dcf(x)dx+∫bdf(x)dx
という具合にして求めることになる.
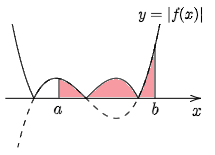
ところでこの面積の合計は,関数全体に絶対値をかぶせた y=|f(x)| を用いれば,次の図2からわかるように,符号を気にすることなく
T=∫ba|f(x)|dx
と表現できる.
まとめ 閉区間 [a, b] で連続な関数 f(x) のグラフと x 軸,及び2直線 x=a,x=b とで囲まれる部分の面積は ∫ba|f(x)|dx
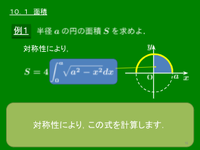
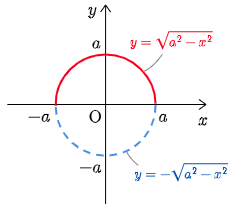
例題1 半径 a の円の面積 S を求めよ.
こたえ
補足
この問題では「半径 a の円の面積を求めよ」であったから,S=4∫a0√a2−x2dx の計算のところで置換積分を行わなければならなかった.入試問題を解いていると,しばしば ∫βα√a2−x2 dx の形の積分計算が必要になるが,そのときには逆に式の意味からこの積分が円の面積(の一部)を表していることに注目して,置換積分を行うのではなく,一気に答えまでもっていくのが実践的である.以下その例をいくつか挙げる.
a>0 のとき
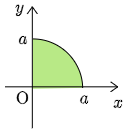
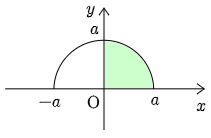
① ∫a0√a2−x2dx=πa24
→ 半径 a の円の面積の 14
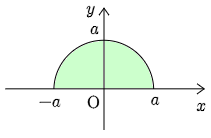
② ∫a−a√a2−x2dx=πa22
→ 半径 a の円の面積の 12
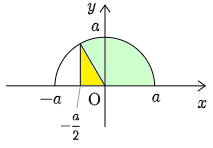
③ ∫a−a2√a2−x2dx=√3a28+πa23
→ 第1項が直角三角形の面積(黄色)
第2項が中心角 120∘ の扇形の面積(緑色)
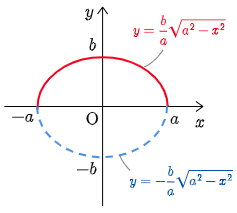
例題2 楕円 x2a2+y2b2=1 (a>0,b>0) の面積 S を求めよ.
答
解答例を表示する
補足
S=πab は半径 a の円の面積の ba 倍となっているが, y=ba√a2−x2 という式を見れば,各 x に対して y の値が,常に円の場合 (√a2−x2) の ba 倍となっているところからも納得できる.

10.2 2曲線に囲まれた部分の面積
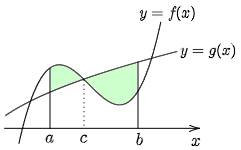
図のような2曲線 y=f(x) と y=g(x) ,及び2直線 x=a,x=b (ただし a<b) で囲まれた部分(図の緑色)の面積 S は,グラフの上下関係を考えると
S=∫ca{f(x)−g(x)}dx−∫bc{f(x)−g(x)}dx
で計算されるが,y=|f(x)−g(x)| というように絶対値をつけておけば,関数の符号を気にすることなく次のようにコンパクトに表現できる.(が実際の計算の段においては,絶対値記号が付いたままでは積分できないので,上のように積分区間を分けて計算することになる.あくまで表現が簡潔になるというだけ.)
2曲線 y=f(x) と y=g(x),及び2直線 x=a, x=b (ただし a<b)で囲まれる部分の面積は ∫ba|f(x)−g(x)|dx
冒頭で関数 y=f(x) のグラフと x 軸,及び2直線 x=a,x=b (ただし a<b) で囲まれた部分の面積が ∫na|f(x)|dx で表されることを見たが,これは x 軸の方程式が y=0 であるから g(x)=0 (定数関数)の特別の場合であったことに過ぎない.
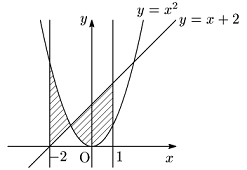
例題 曲線 y=x2(−2≦x≦1) と3直線 y=x+2, x=−2, x=1 で囲まれる部分の面積 S を求めよ.
答
解答例を表示する
10.3 媒介変数(パラメータ)表示と面積
ポイント 媒介変数(パラメータ)を消去せず,そのままの形を生かす: ∫ydx=∫ydxdtdt (置換積分)
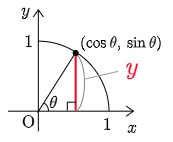
例題1 半径1の円の面積 S を求めよ.
答
解答例を表示する
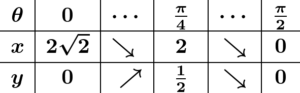
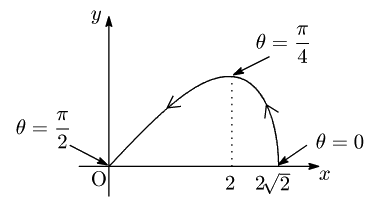
例題2 曲線 {x=2√2cosθy=12sin2θ (0≦θ≦π2) と x 軸とで囲まれた部分の面積Sを求めよ.
答
解答例を表示する
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | 問題 | |
| 1. 不定積分 | [無料] | ||
| 2. 置換積分法(不定積分) | [無料] | ||
| 3. 部分積分法(不定積分) | [無料] | ||
| 4. 定積分とその性質 | [会員] | ||
| 5. 置換積分法(定積分) | [会員] | ||
| 6. 部分積分法(定積分) | [会員] | ||
| 7. 定積分と微分法 | [会員] | ||
| 8. 定積分と和の極限 | [会員] | ||
| 9. 定積分と不等式 | [会員] | ||
| 10. 定積分の応用(面積) | [会員] | ||
| 11. 定積分の応用(体積) | [会員] | [会員] | |
| 12. 定積分の応用(回転体の体積) | [会員] | ||
| 13. 曲線の長さ |