高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
1．中線とは
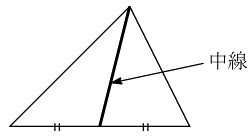
三角形の頂点と，その頂点に対応する辺の中点とを結んだ線分を中線という．三角形には3本の中線がある．
2．重心
2本の直線は平行でなければ必ず1点で交わる．ところがここにもう1本追加して3本の直線を考えると，必ずしも1点で交わるとは限らない．
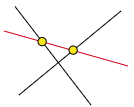
ところが三角形においてはその形状にかかわらず，いつでも例外なく3本の中線が1点で交わるというのである．
定理
三角形の3本の中線は1点で交わり，その点は各中線を$2:1$に内分する．
三角形の3本の中線は1点で交わり，その点は各中線を$2:1$に内分する．
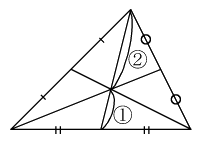
3本の中線が1点で交わる
補足
三角形の重心とは
3中線の交点を，三角形の重心という．
証明の方針
- この証明に使う道具は，中点連結定理と平行線と線分の比の関係．
- 3本の中線から2本組を選びその交点をG，別の組の交点をG$\,’$ とする．GとG$\,’$ が一致することを示す．
↓どうやって？
中点連結定理を用いて，AG:GLとAG$\,’$:G$\,’$Lが共に2:1であることを示す．
証明
△ABCにおいて，辺BC，CA，ABの中点をそれぞれL，M，Nとし，
中線ALとBMの交点をG
中線ALとCNの交点をG$\,’$
とする．
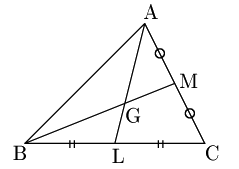
まずGについて
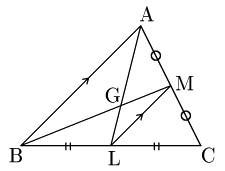
M，Lはそれぞれ辺CA，CBの中点だから，△CABにおいて中点連結定理により，
\[{\rm ML}//{\rm AB},\ {\rm ML}=\frac12{\rm AB}\]よって，
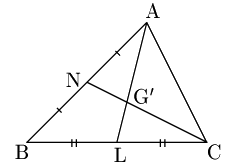
\[{\rm AG}:{\rm GL}={\rm AB}:{\rm ML}=2:1\ \ \cdots\mbox{①}\]次にG$\,’$ について
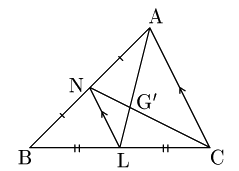
N，Lはそれぞれ辺BA，BCの中点だから，△BACにおいて中点連結定理により，
\[{\rm NL}//{\rm AC},\ {\rm NL}=\frac12{\rm AC}\]よって，
\[{\rm AG\,’}:{\rm G\,’L}={\rm AC}:{\rm NL}=2:1\ \ \cdots\mbox{②}\]①，②より，2点GとG$\,’$ は同じ点であるから，3つの中線は1点で交わり，
$\boldsymbol{{\rm AG}:{\rm GL} =2:1}$
同様にして，BG:GM=2:1，CG:GN=2:1も示される．
■
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |