「チェバの定理の逆」の内容を確認し,証明していきます.
チェバの定理は,三角形の辺あるいはその延長上にない1点と各頂点とを結ぶ3直線があり,それら3直線と各辺との3つの交点についてある関係式が成り立つというものでした.
その逆命題である「チェバの定理の逆」とは,三角形の各辺あるいはその延長上に1点ずつ計3個の点を取っておき,それらの点と対応する頂点を結ぶ3直線について,ある関係式を満たせばそれら3直線が1点で交わるというものです.
最初にとる3点が,すべて辺上である場合と,1点のみが辺上である場合に分けて証明していきます.分けて証明はするものの,実のところ図が異なるだけで,式や説明文は一字一句同じなのです.
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

3.チェバの定理の逆
| 3.1 チェバの定理の逆 | スライド① |
| 3.1 チェバの定理の逆(続き) | スライド② |
| 3.1 チェバの定理の逆(続き) | スライド③ |
スライドはぜひ全画面表示で
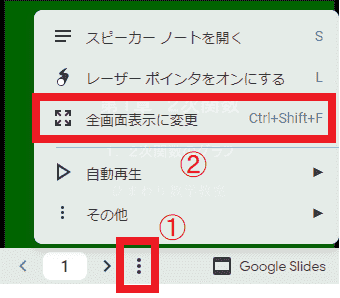
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
スライド① チェバの定理の逆
スライド② チェバの定理の逆(続き)
スライド③ チェバの定理の逆(続き)

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
