数学A　第3章　図形の性質

  スライド ノート 問題
1. チェバの定理 [無料]   [会員]
2. メネラウスの定理 [無料]   [会員]
3. チェバの定理の逆 [無料]    
4. メネラウスの定理の逆 [会員]    
5. 円に内接する四角形 [会員]   [会員]
6. 接弦定理とその逆 [会員]    
7. 方べきの定理とその逆 [会員]    
8. 三角形の五心      
　　重心      
　　外心      
　　垂心      
　　内心      
　　傍心      

中学校の範囲

  スライド ノート 問題
1. 円周角の定理     [会員]
2. 円周角の定理の逆     [会員]

演習問題

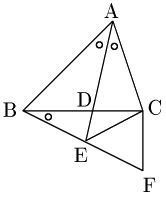
問題１【発展】
　△ABCにおいて，∠BACの二等分線と辺BCの交点をDとし，ADの延長上に点Eを$\angle{\rm BAD}=\angle{\rm DBE}$ となるようにとる．また，BEの延長上に ${\rm BE=EF}$ となる点Fをとるとき，$\angle{\rm BCF=90^\circ}$ となることを示せ．

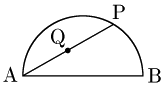
問題２【発展】
　${\rm AB=6cm}$ である線分ABを直径とする半円の弧上を，点PがAからBまで動くとき，線分APの中点 $\rm Q$ の軌跡の長さを求めよ．

問題１【発展】

　△ABCにおいて，∠BACの二等分線と辺BCの交点をDとし，ADの延長上に点Eを$\angle{\rm BAD}=\angle{\rm DBE}$ となるようにとる．また，BEの延長上に ${\rm BE=EF}$ となる点Fをとるとき，$\angle{\rm BCF=90^\circ}$ となることを示せ．

解答