高校数学[総目次]

数学A　第3章　図形の性質

  スライド ノート 問題
1. チェバの定理      
2. メネラウスの定理      
3. チェバの定理の逆      
4. メネラウスの定理の逆      
5. 円に内接する四角形      
6. 接弦定理とその逆      
7. 方べきの定理とその逆      
8. 三角形の五心      
　　重心      
　　外心      
　　垂心      
　　内心      
　　傍心      

中学校の範囲

  スライド ノート 問題
1. 円周角の定理      
2. 円周角の定理の逆      

演習問題

問題１【基本】
　次の図において，∠x, ∠y の大きさをそれぞれ求めよ．ただし点Oは円の中心である．

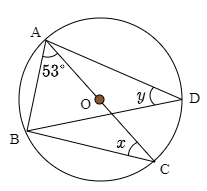
問題２【基本】
　次の図において，∠x, ∠y の大きさをそれぞれ求めよ．ただし点Oは円の中心である．

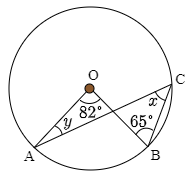
問題３【基本】
　次の図において，弧ABと弧CDは長さが等しいとき，四角形ABCDは台形であることを示せ．

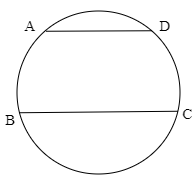
問題４【標準】
　次の図において，円の半径は4cmとする．このとき弧AB(Cを含まない方)の長さを求めよ．

問題１【基本】

　次の図において，∠x, ∠y の大きさをそれぞれ求めよ．ただし点Oは円の中心である．

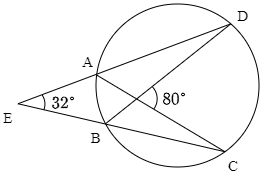
解答

　弦ACは直径ですから，∠ABC は直角です．ポイント
　従って△ABCの内角を考えて，

∠x=90∘−53∘=37∘

　また，弧ABに対する円周角より

∠y=∠x=37∘

問題２【基本】

　次の図において，∠x, ∠y の大きさをそれぞれ求めよ．ただし点Oは円の中心である．

解答

　弦ABに対する円周角である x は，その中心角である 82∘ の半分ですから，∠x=41∘．

　また図中の2つの三角形の内角と外角の関係により