高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

1.中心角
円の中心と,弧の両端を結んでできる図の角(赤色)を,その弧(水色)に対する中心角という.
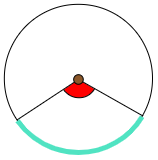
この表現からわかるように,中心角は弧に対応したものであって,弦に対応したものではないことに注意しよう.その理由は以下に示すように,中心角と弧は比例関係にあるが,中心角と弦は比例関係にないからである.
1つの円で,2つの中心角とそれらに対応した弧について次が成り立つ.
定理
中心角が等しい ⟺ 弧の長さが等しい
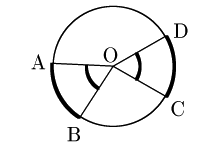
証明
中心角が等しいとき,回転移動させると2つの扇形はぴったりと重なるから,弧の長さも等しい.
弧の長さが等しいとき,回転移動させると2つの扇形はぴったりと重なるから,中心角も等しい.

回転させるとぴったりと重なる
■
上の定理から,中心角を2倍,3倍とすれば,弧の長さも2倍,3倍になる.
逆に,弧の長さを2倍,3倍とすれば,中心角も2倍,3倍となる.
一般に次が成り立つ:
注意
弦の長さは中心角に比例しない.

円周上の2点A,Bに対して「弧AB」というとき,それが指すものは短い方とそうでない方の2つある.短い方の弧を劣弧という.
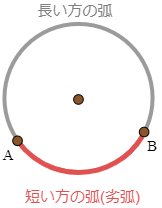
弧を長くない方に制限すると次が成り立つ.
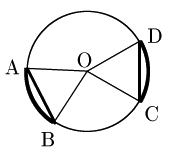
証明
「弧の長さが等しい ⟹ 弦の長さが等しい」を示す.
弧の長さが等しいならば,上の定理 により中心角が等しい.よって2つの二等辺三角形OABとOCDは合同である.(∵ 2辺夾角相等)
従って対応する辺(弦)の長さが等しい.
「弧の長さが等しい ⟸ 弦の長さが等しい」を示す.
弦の長さが等しいならば,2つの二等辺三角形OABとOCDは合同である.(∵ 3辺相等)
従って対応する角(中心角)が等しいから,上の定理 により弧の長さが等しい.
■
補足
上の定理で弧を劣弧に制限していないと,
弧の長さが等しい ⟹ 弦の長さが等しい
の方は常に成り立つが,逆の
弧の長さが等しい ⟸ 弦の長さが等しい
の方は必ずしも成り立たない.「弦AB」に対して「弧AB」には長い方と短い方の2つがあるからである.

2.円周角の定理
図のように,円周上の1点と,弧の両端を結んでできる角(赤色)を,その弧(水色)に対する円周角という.また逆に水色の弧を,赤色の円周角に対する弧という.
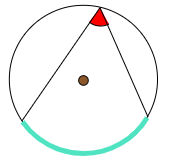
中心角のときと同様に,円周角と対応しているものは弧であって弦ではない.その理由は,弧と円周角には次に示す円周角の定理と呼ばれる重要な関係があるからである.
- 同じ弧に対する円周角は等しい.
- (円周角) =12×(中心角)
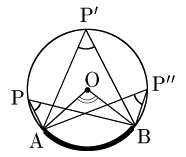
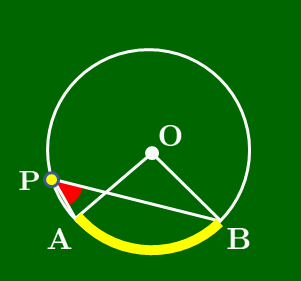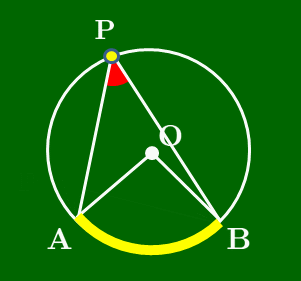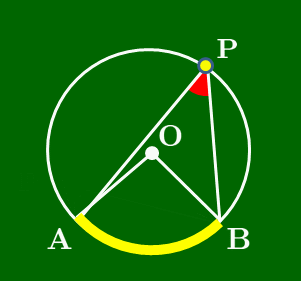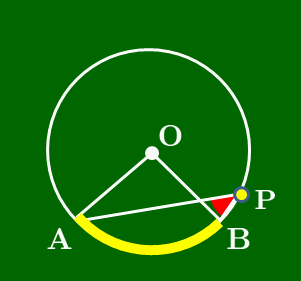
∠APB(赤色)の大きさはどれも同じ
証明の流れ
- 1.「(円周角) =12×(中心角)」を示す.
- 円の中心Oがどの位置にあるかで3通りに場合分け.
- 2.「同じ弧に対する円周角は等しい」を示す.
- 中心角を経由して示す.
証明
まず「(円周角) =12×(中心角)」を示す.
[1] 中心Oが∠APBの内側にあるとき
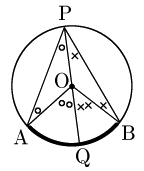
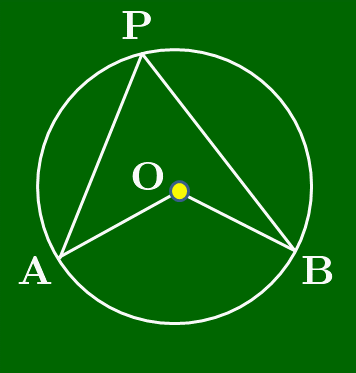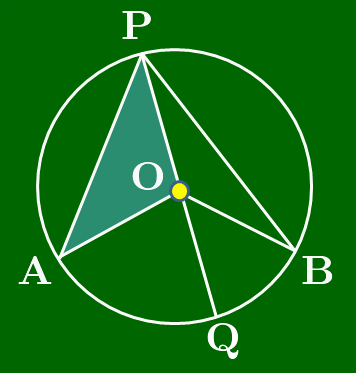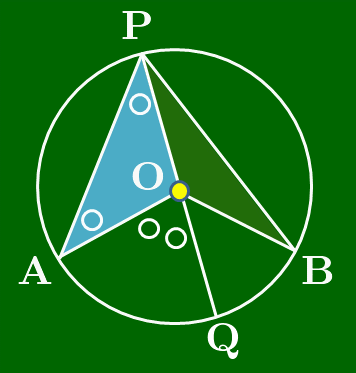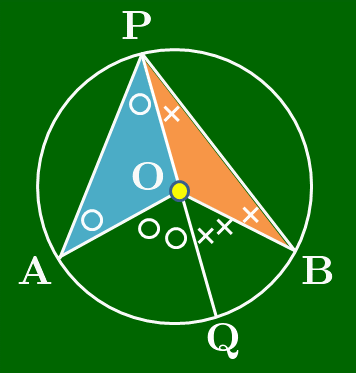
図のように直径PQをとると,三角形の内角と外角の関係により, ∠AOQ=2 ∠APO ⋯①∠BOQ=2 ∠BPO ⋯② よって, ∠AOB=∠AOQ+∠BOQ=2 ∠APO+2 ∠BPO (∵①,②)=2 (∠APO+∠BPO) (2でくくった)=2 ∠APB ∴∠APB=12∠AOB
[2] 中心Oが線分APまたはBP上にあるとき
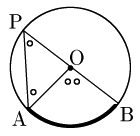
三角形の内角と外角の関係より∠APB=12∠AOB.
[3] 中心Oが∠APBの外側にあるとき
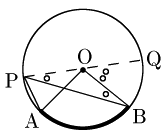
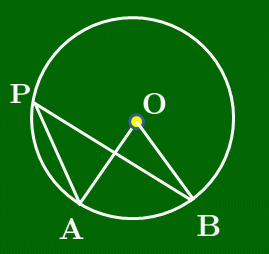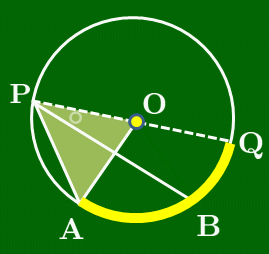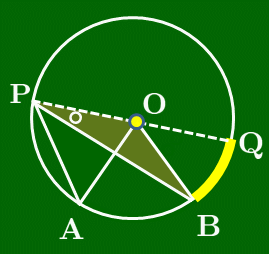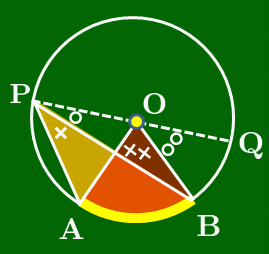
図のように直径PQをとると,弧AQについて ∠APQ=12∠AOQ ⋯① が成り立つ(∵[2]).同様に弧BQについても ∠BPQ=12∠BOQ ⋯② が成り立つ.よって, ∠APB=∠APQ−∠BPQ=12∠AOQ−12∠BOQ (∵①,②)=12(∠AOQ−∠BOQ) (12でくくった)=12∠AOB
以上により, (円周角)=12×(中心角) が示された.
次に「同じ弧に対する円周角は等しい」を示す.
同じ弧に対する円周角は,常にその弧の中心角の半分であるからどれも等しい.
以上により,円周角の定理が示された.
補足
円周角の定理から直ちに次が成り立つ:
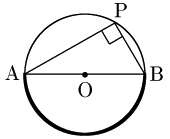
証明
半円の弧に対する中心角は180°であるから,円周角の定理により円周角はその半分の90°である.

3.弧と円周角
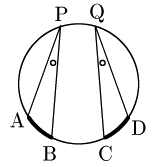
証明の概要
「中心角が等しい ⟺ 弧の長さが等しい」及び「(円周角) =12× (中心角)」を利用して示す.
証明
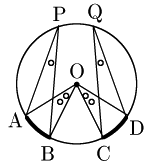
円周角が等しい
⟺ 中心角が等しい(∵円周角の定理 )
⟺ 弧の長さが等しい (∵上の定理 )

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
