数学A 第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [無料] | [会員] | |
| 2. メネラウスの定理 | [無料] | [会員] | |
| 3. チェバの定理の逆 | [無料] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
演習問題
四角形が円に内接するということは，換言すれば4点が同一円周上にあるということです．4点が同一円周上にあるかどうか判定する問題に対処するためのトレーニングを中心にしていきましょう．
問題１【標準】
四角形ABCDはAD//BCの台形である．図のように2点A，Dを通る円と2辺AB，CDとの交点をそれぞれE，Fとすると，4点E，B，C，Fは同一円周上にあることを示せ．
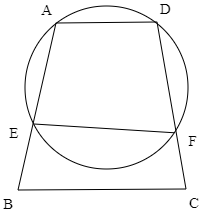
問題２【発展】
図のように円Oと，円Oの中心を通るもう一つの円があり，2点A，Bで交わっている．Aを通る直線が2点とC，Dで交わっているとき，BD=CDであることを示せ．
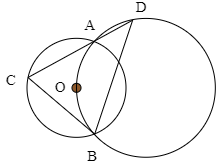
問題３ 共通テスト対策！
図において，4点A，B，C，Dは同一円周上にあること示せ．
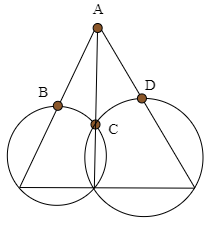
問題４【発展】
図のような円に内接する四角形ABCDにおいて，ADとBCの延長線の交点をE，ABとCDの延長線の交点をFとする．△CDEの外接円とEFの交点をGとするとき，4点F，B，C，Gは同一円周上にあることを示せ．
問題１【標準】
四角形ABCDはAD//BCの台形である．図のように2点A，Dを通る円と2辺AB，CDとの交点をそれぞれE，Fとすると，4点E，B，C，Fは同一円周上にあることを示せ．
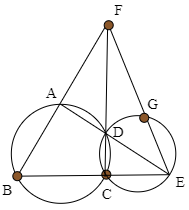
解答
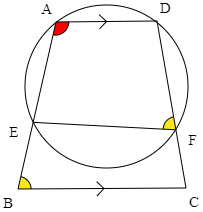
台形ABCDにおいて，AD//BCより