高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

1.円に内接する四角形
三角形には外接円が必ず存在する(外心 参照).つまり三角形ならどんなものでも円に内接することができるのであるが,ここにもう1点追加して四角形にすると,もはや円に内接することは保証されない.1つの三角形に対して外接円はただ1つに決定されるが,残りの1点はこの外接円上に限らずどこにでも存在する可能性があるからだ.以下で四角形が円に内接するための条件,換言すると4点が同一円周上にあるための条件を確認していくのであるが,四角形が円に内接する条件はこれ以外にもいくつかの言い換えがある.それらの筆頭ともいえるほど重要なのが,次の定理である.四角形が円に内接するかどうかの判定は,共通テスト等でも問われる可能性が大いにある.定理の内容が理解出来たら演習問題 で実践トレーニングを行っておこう.
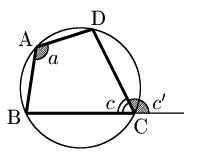
⟺ 対角の和が180° (a+c=180∘)
⟺ 内角が,その対角の外角に等しい (a=c′)
証明の方針
- 「四角形が円に内接する ⇒ 対角の和が180°」は,円周角の定理 を利用.
- 「四角形が円に内接する ⇐ 対角の和が180°」は,△ABDの外接円上点C′ をとり,円周角の定理の逆 を利用.
- 「対角の和が180°⟺内角が,その対角の外角に等しい」は明らか.
証明
「四角形が円に内接する ⇒ 対角の和が180°」を示す.
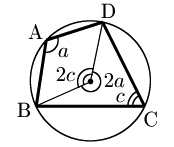
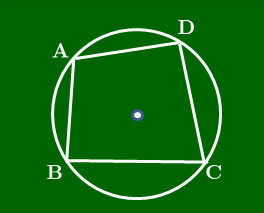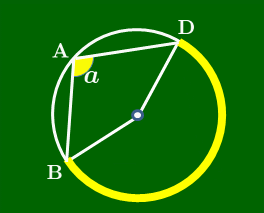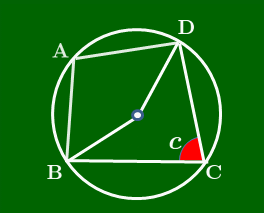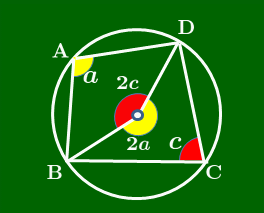
円周角の定理 により図のようになるから,中心角に注目すると, 2a+2c=360∘ ∴a+c=180∘
「四角形が円に内接する ⇐ 対角の和が180°」を示す.
∠A+∠C=180∘ ⋯① であるような四角形ABCDを考える:
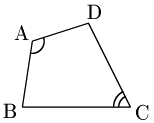
△ABDの外接円Oにおいて,下図のように弧BD上に点C ′ をとる.
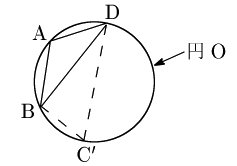
四角形ABC′Dは円に内接するから,先に示した事柄により,
∠A+∠C′=180∘ ⋯②
である.
①,②より,∠C=∠C′.
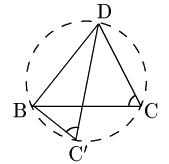
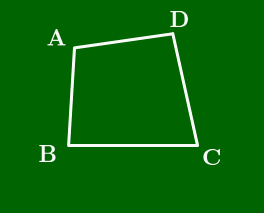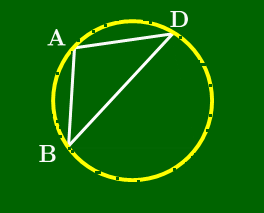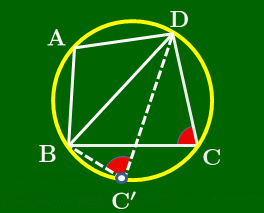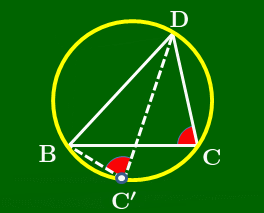
2点C,C′ が直線BDについて同じ側にあるから,円周角の定理の逆 により4点B,C′,C,Dは同一円周上,即ち円O上にある.
故に四角形ABCDは円Oに内接するから4点A,B,C,Dは同一円周上にある.
残るは「対角の和が180°⟺内角が,その対角の外角に等しい」の証明であるが,これは明らか.
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |