このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

  スライド ノート 問題
1. チェバの定理 [会員]   [会員]
2. メネラウスの定理 [会員]   [会員]
3. チェバの定理の逆 [会員]    
4. メネラウスの定理の逆 [会員]    
5. 円に内接する四角形 [会員]   [会員]
6. 接弦定理とその逆 [会員]    
7. 方べきの定理とその逆 [会員]    
8. 三角形の五心      
　　重心      
　　外心      
　　垂心      
　　内心      
　　傍心      
中学校の範囲
  スライド ノート 問題
1. 円周角の定理     [会員]
2. 円周角の定理の逆     [会員]

1．チェバの定理

チェバの定理とは

　三角形と3つの線分で構成された図形で成り立つチェバの定理を見ていこう．この線分の一端は三角形の頂点で，もう一端は辺上，または辺の延長上である．そして何よりその3線分が1点で交わっているということが必要である．次に示す定理の中では，先に交点となるべき点をとっておいて，各頂点とその点を結ぶ反直線が，三角形の辺またはその延長上と交わる点を考えている．(すぐ下のアニメーション参照．)

チェバの定理
　直線AB，BC，CA上にない点Oをとる．△ABCの頂点A，B，Cと点Oを結ぶ各直線が対辺，またはその延長とそれぞれP，Q，Rで交わるとき，次が成り立つ： \[\boldsymbol{\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1}\]
点O が△ABC の内部にあるとき
点O が△ABC の外部にあるとき
アニメーション
(スライドから抜粋)
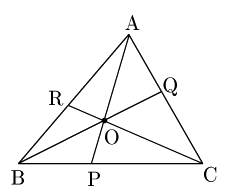
点が△ABCの内部にある場合
アニメーション
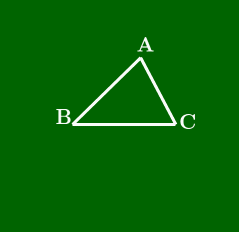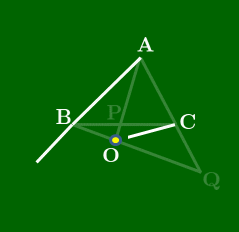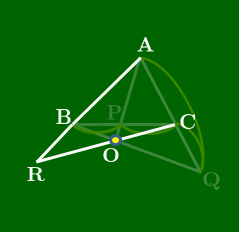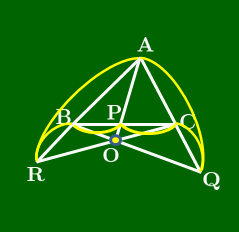
(スライドから抜粋)
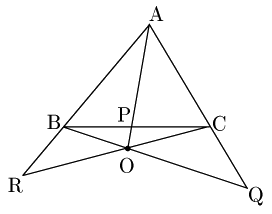
点が△ABCの外部にある場合

証明のポイント

　3つの線分比の値(分数)を，三角形の面積比の値で表す．

確認事項

  • 　比 $a:b$ について，$\dfrac ab$ を比の値という．$\dfrac ab=\dfrac cd$ が成り立つとき，$a:b=c:d$ と表す．

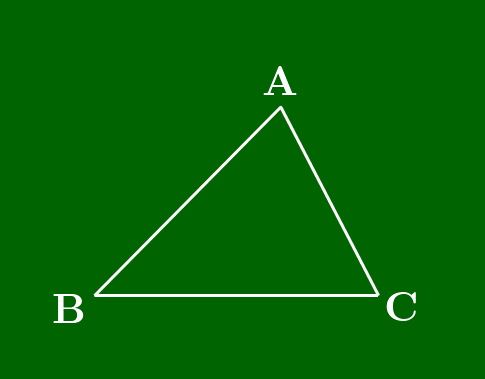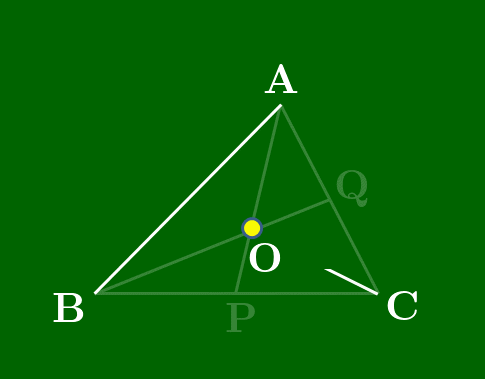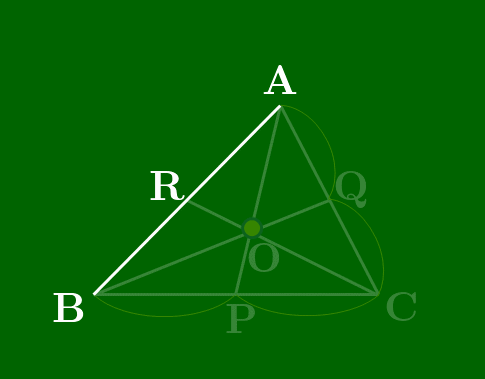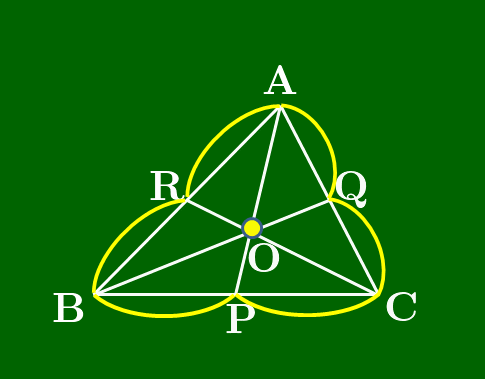
証明

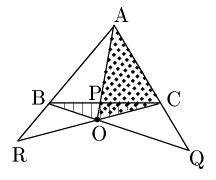
1°　点Oが△ABCの内部にあるとき

辺OAが共通の底辺→高さの比が面積比

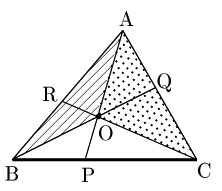
　まず，BP：PCは，△OAB(斜線部)と△OCA(打点部)の面積比と一致する．何故なら線分AOを共通の底辺とみれば，面積比は高さの比に等しく，高さの比はBP：PCに等しいからである．（詳しくはスライド 参照）

　従って

\[\rm BP:PC=\triangle OAB:\triangle OCA\]

$\therefore \dfrac{\rm BP}{\rm PC}=\dfrac{\triangle \rm OAB}{\triangle \rm OCA}\ \ \cdots$ ①

　次にCQ：QAであるが，先ほどと同様に考えて△OCB(破線部)と△OAB(斜線部)の面積比に等しい(下図)．

辺OBが共通の底辺→高さの比が面積比

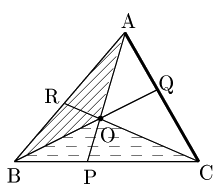
　従って

$\dfrac{\rm CQ}{\rm QA}=\dfrac{\triangle \rm OCB}{\triangle \rm OAB}\ \ \cdots$ ②

　最後にAR：RBも，これまでと同様に考えて△OCA(打点部)と△OCB(破線部)の面積比に等しい(下図)．

辺OCが共通の底辺→高さの比が面積比

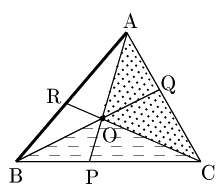
　従って

$\dfrac{\rm AR}{\rm RB}=\dfrac{\triangle \rm OCA}{\triangle \rm OCB}\ \ \cdots$ ③

　①，②，③を辺々掛けて

\[\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=\frac{\triangle \rm OAB}{\triangle \rm OCA}\cdot\frac{\triangle \rm OCB}{\triangle \rm OAB}\cdot\frac{\triangle \rm OCA}{\triangle \rm OCB}\]

　右辺が次々と約分できて

\[\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1\]

2°　点Oが△ABCの外部にあるとき

　点Oが△ABCの内部にある場合とは図が異なるだけで，式は異なるところが1つもない．

辺OAが共通の底辺→高さの比が面積比

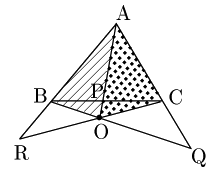
　BP：PCは，△OABと△OCAの面積比と一致する．何故なら線分AOを共通の底辺とみれば，面積比は高さの比に等しく，高さの比はBP：PCに等しいからである．（詳しくはスライド 参照）

　従って

\[\rm BP:PC=\triangle OAB:\triangle OCA\]

$\therefore \dfrac{\rm BP}{\rm PC}=\dfrac{\triangle \rm OAB}{\triangle \rm OCA}\ \ \cdots$ ④

　次にCQ：QAであるが，先ほどと同様に考えて△OCBと△OABの面積比に等しい(下図)．

辺OBが共通の底辺→高さの比が面積比

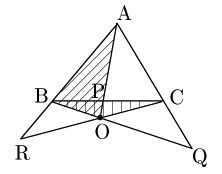
　従って

$\dfrac{\rm CQ}{\rm QA}=\dfrac{\triangle \rm OCB}{\triangle \rm OAB}\ \ \cdots$ ⑤

　最後にAR：RBも，これまでと同様に考えて△OCAと△OCBの面積比に等しい(下図)．

辺OCが共通の底辺→高さの比が面積比

　従って

$\dfrac{\rm AR}{\rm RB}=\dfrac{\triangle \rm OCA}{\triangle \rm OCB}\ \ \cdots$ ⑥

　④，⑤，⑥を辺々掛けて

\[\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=\frac{\triangle \rm OAB}{\triangle \rm OCA}\cdot\frac{\triangle \rm OCB}{\triangle \rm OAB}\cdot\frac{\triangle \rm OCA}{\triangle \rm OCB}\]

　右辺が次々と約分できて

\[\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1\]

■

補足

  • [覚え方] 分子→分母→分子→分母→ … という順でアルファベットがしりとり式に続いていく．
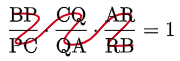
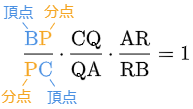
  • [書き方] 加えて，頂点→分点→頂点→分点→… の順でアルファベットを書く．
  • [融通性] チェバの定理の左辺は3つの分数の積になっている．積は計算の順序が自由にできるから，掛ける順番をローテーションして\[\begin{align*}&\dfrac{\rm BP}{\rm PC}\cdot\dfrac{\rm CQ}{\rm QA}\cdot\dfrac{\rm AR}{\rm RB}\\[5pt]=&\dfrac{\rm AR}{\rm RB}\cdot\dfrac{\rm BP}{\rm PC}\cdot\dfrac{\rm CQ}{\rm QA}\\[5pt]=&\dfrac{\rm CQ}{\rm QA}\cdot\dfrac{\rm AR}{\rm RB}\cdot\dfrac{\rm BP}{\rm PC}\end{align*}\]などが成り立つ．つまり，スタート地点は頂点Bである必要はなく，三角形の3頂点のどれでもよい．
  • チェバの定理とメネラウスの定理 は式が完全に同一である．

コラム　チェバの定理は覚えにくい！？

　チェバの定理の式は

\[\frac{\rm BP}{\rm PC}\cdot\frac{\rm CQ}{\rm QA}\cdot\frac{\rm AR}{\rm RB}=1\]

となっていて，日本語で「(PC 分の BP) × (QA 分の CQ) …」と読んでいると，三角形の頂点・分点をしりとり式にひと筆ふで書きで追えなくなります．この式の両辺の逆数をとれば

\[\frac{\rm PC}{\rm BP}\cdot\frac{\rm QA}{\rm CQ}\cdot\frac{\rm RB}{\rm AR}=1\]

となり，これならば私たちの言い回し通りにきれいに輪を描くように一周できます．しかしどういう訳か教科書では最初に書いた表現となっています．

　この理由を想像するに，恐らくですが英語での表現に基づいているのではないかと思います．$\dfrac{\rm BP}{\rm PC}$ を例にとると英語では「BP over PC」という言い方があります．つまり分子が先，分母が後になっているのです．このように「〇〇 over △△」と読みながら，分子から先に書くようにすれば，輪を描くようにして教科書と同様の式が書きやすくなります．次に学ぶメネラウスの定理でも同様です．すぐに慣れて違和感なく書けるようになるでしょう．

定理の内容が理解出来たら，次は演習問題 で理解の確認！

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学A　第3章　図形の性質

第3章　図形の性質

  スライド ノート 問題
1. チェバの定理 [会員]   [会員]
2. メネラウスの定理 [会員]   [会員]
3. チェバの定理の逆 [会員]    
4. メネラウスの定理の逆 [会員]    
5. 円に内接する四角形 [会員]   [会員]
6. 接弦定理とその逆 [会員]    
7. 方べきの定理とその逆 [会員]    
8. 三角形の五心      
　　重心      
　　外心      
　　垂心      
　　内心      
　　傍心      
中学校の範囲
  スライド ノート 問題
1. 円周角の定理     [会員]
2. 円周角の定理の逆     [会員]