高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | [会員] | ||
| 2. 直線の方程式 | [会員] | ||
| 3. 円の方程式 | [会員] | [会員] | |
| 4. 円と直線 | [会員] | [会員] | |
| 5. 軌跡と方程式 | [会員] | [会員] | |
| 6. 不等式と領域 | [会員] |

演習問題
問題1【発展】
放物線 と直線 が2つの異なる2つの交点をもつとする.
(1) 2つの交点を結ぶ線分を直径とする円の方程式を求めよ.
(2) 放物線 と(1)で求めた円の交点が4つあるための条件を求めよ.
(名古屋市立大・一部抜粋)

(1) 円の方程式を得るためには,円の中心と半径の情報が必要です.とりあえず交点の座標を求めてみましょう.(2)では,4次方程式を解くことになりますが,4つの解のうち2つは既にわかっているので因数分解が可能です.
解答
(1) より .放物線と直線が異なる2つの交点をもつから が必要で,このとき .従って円の中心は原点であり,半径は である.よって求める円の方程式は
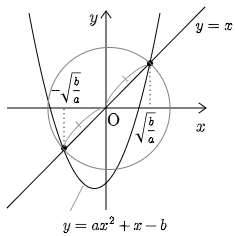
(2) を に代入して を消去すると
右辺の分母を払って整理すると
いかにも手ごわい方程式に見えますが,放物線 と直線 の交点の 座標である はこの方程式の解でもありますから,この方程式の左辺は を導く元となった ,即ち の左辺を因数にもちます.ポイント①
(1)よりこの式の左辺は を因数にもつから,実際に割って商を求めて因数分解すると
題意はこの4次方程式が異なる4つの実数解をもつことと同値であるから,方程式① の判別式を とすると が必要で,
ここからは方程式① の解が と重なっていないかどうかをチェックします.このチェック方法は定石の1つとしてマスターしておきましょう.ポイント②
ここで,方程式① が 又は を解にもつとすれば,
両辺を2乗して
故に, であれば,4次方程式 は異なる4つの実数解をもつから,これが求める条件である.
