高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | [会員] | ||
| 2. 直線の方程式 | [会員] | ||
| 3. 円の方程式 | [会員] | [会員] | |
| 4. 円と直線 | [会員] | [会員] | |
| 5. 軌跡と方程式 | [会員] | [会員] | |
| 6. 不等式と領域 | [会員] |

2.1 直線の方程式
[1] 傾き m,y 切片 n の直線
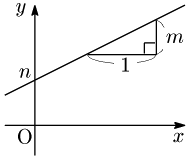
y=mx+n
[2] 点A(x1,y1) を通り,傾き m の直線
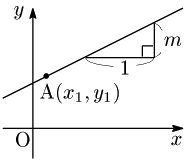
求める直線 :y=mx+n ⋯ ①
これがAを通る:y1=mx1+n ⋯ ②
① – ②より,y−y1=m(x−x1)
y−y1=m(x−x1)
検証
(x,y)=(x1,y1) は確かにこの式を満たす.また,この式を変形すると, y=mx−mx1+y1 となり,m と −mx1+y1 はともに定数であるから直線を表す.
[3] 2点A(x1,y1),B(x2,y2) を通る直線
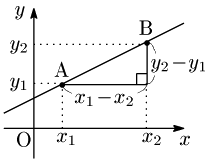
1∘ x1≠x2のとき_
傾き:y2−y1x2−x1
よって [2] より,
y−y1=y2−y1x2−x1(x−x1) ⋯(∗)
補足
2点 A, B の位置関係は,次のいずれであっても上の式で表される.
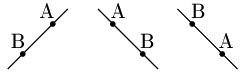
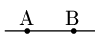
また,y1=y2 のとき,直線は x 軸に平行になるが,この場合も上の式で表すことができて,
y=y1
2∘ x1=x2のとき_
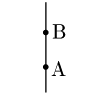
直線は x 軸に垂直であり,(∗) の式で表すことができない.このとき直線の方程式は,
x=x1
まとめ
傾き m,y 切片 n の直線:y=mx+n
点(x1,y1)を通り,傾きm の直線:y−y1=m(x−x1)
2点(x1,y1), (y2,y2) を通る直線:
x1≠x2 のとき,y−y1=y2−y1x2−x1(x−x1)x1=x2 のとき,x=x1
例題 2点 (1,1), (3,5) を通る直線の方程式を求めよ.
答
y−1=5−13−1(x−1) ∴y=2x−1_
別解
y−5=5−13−1(x−3) ∴y=2x−1_
補足
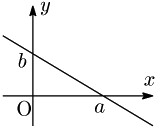
a≠0,b≠0 とする.2点 (a,0),(0,b) を通る直線の方程式は, y=−bax+b ∴bax+y=b 両辺を b で割って次を得る:
xa+yb=1
例題 2点 (3,0), (0,2) を通る直線を求めよ.
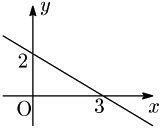
答
x3+y2=1_ (y=−23x+2)
直線の方程式の一般形
一般に,x と y の1次方程式
ax+by+c=0 ⋯ ①
(ただし,a≠0 または b≠0)
のグラフは直線である.
逆に,直線の方程式はすべて①の形で表すことができる.

2.2 2直線の関係
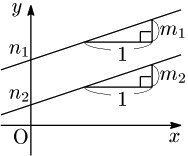
[1] 平行条件
2直線 y=m1x+n1⋯①,y=m2x+n2⋯②について,①//②⟺m1=m2
例題 点 (1,4) を通り,直線 y=−2x+1 に平行な直線を求めよ.
答 傾きが −2 で,点 (1,4) を通る直線だから, y−4=−2(x−1)∴y=−2x+6
[2] 垂直条件
2直線 y=m1x+n1⋯①,y=m2x+n2⋯②について,①⊥②⟺m1m2=−1
証明
2直線①,②にそれぞれ平行な直線
y=m1x ⋯ ①′,y=m2x ⋯ ②′
が垂直に交わる場合を考えれば十分.
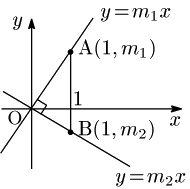
2直線①′,②′上で,x 座標が1である点をそれぞれA,Bとすると, ①′⊥②′⟺∠AOB=90∘⟺OA2+OB2=AB2 (三平方の定理)⟺(12+m12)+(12+m22)=(m1−m2)2⟺m1m2=−1
■
例題 直線 y=2x+5に垂直な直線の傾きを求めよ.
答
求める直線の傾きを m とすると,
2×m=−1 ∴m=−12_
発展的補足
2直線 a1x+b1y+c1=0⋯①,a2x+b2y+c2=0⋯②について,①//②⟺a1b2−a2b1=0①⊥②⟺a1a2+b1b2=0
証明
b1≠0 かつ b2≠0 の場合を示す.
①より y=−a1b1x−c1b1
②より y=−a2b2x−c2b2
よって,
①//②⟺−a1b1=−a2b2⟺a1b2−a2b1=0①⊥②⟺−a1b1⋅(−a2b2)=−1⟺a1a2+b1b2=0
■
※ 上の関係は,b1=0 または b2=0 のケースも含めて,ベクトルの内積を用いて示すのが簡潔.
[3] 一致条件
2直線 a1x+b1y+c1=0,a2x+b2y+c2=0 が一致する条件は, a2a1=b2b1=c2c1 ただし,分子か分母の一方でも0のときは,他方も0.
注意
一致条件は,a1=a2,b1=b2,c1=c2 ではない.
例えば,x+2y+3=0 と 2x+4y+6=0 は同じ直線を表す.

2.3 直線に関して対称な点
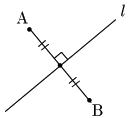
⟺ AB ⊥l かつ 線分ABの中点が l 上
例題 直線 l:y=2x−1 に関して,点A(0,4) と対称な点B(p,q) を求めよ.
答
AB⊥l:_
q−4p−0⋅2=−1 ∴p+2q=8 ⋯ ①
線分ABの中点がl上:_
4+q2=2⋅0+p2−1 ∴2p−q=6 ⋯ ②
①,②より,p=4, q=2.
よって,B(4,2)_

2.4 2直線の交点を通る直線
Q. k を定数として, k(x−y−1)+x+2y−4=0 ⋯(∗) はどんな図形を表すか?
A. 2直線 x−y−1=0, x+2y−4=0 の交点を通る直線を表す.
検証
1° 直線を表すことについて
(∗)を整理すると, (k+1)x+(−k+2)y+(−k+4)=0 これは a,b,c を定数として, ax+by+c=0 の形をしている.
また,x と y の係数は同時には0にならない.
従って,(∗)は直線を表す.
2° 2直線の交点を通ることについて
2直線 x−y−1=0,x+2y−4=0 の交点の座標は (2,1).これを(∗)に代入すると, k(2−1−1)+2+2⋅1−4=0 これは k の値によらず成り立つ.従って(∗)は常に2直線の交点を通る.
一般には次が成り立つ:
2直線 a1x+b1y+c1=0, a2x+b2y+c2=0 が交わるとき,交点を通る直線の方程式は,k を定数として k(a1x+b1y+c1)+a2x+b2y+c2=0 ⋯(☆) と書ける.
注意
(☆)は k の値が決まれば1つの直線が定まる.直線を決定するには2直線の交点の他に,もう1つ通る点 (p,q) を指定すればよい.そのことで k の値が定まる: k(a1p+b1q+c1)+a2p+b2q+c2=0 ⋯① ここで,点 (p,q) が直線 a1x+b1y+c1=0 上になければ,a1p+b1q+c1≠0 であるから, k=−a2p+b2q+c2a1p+b1q+c1 一方,点 (p,q) が直線 a1x+b1y+c1=0 上にあるならば,a1p+b1q+c1=0,a2p+b2q+c2≠0 となるから,①を満たす k は存在しない. このとき,2直線の交点と点 (p,q) を通る直線とは直線 a1x+b1y+c1=0 にほかならない.つまり,
例題 2直線 8x−2y−19=0⋯①, 2x−6y+9=0⋯② の交点と,点(−2,10)を通る直線の方程式を求めよ.
解1 [平凡には]
①,②を連立して,(x,y)=(3,52)
よって, y−10=52−103−(−2)(x+2) ∴y=−32x+7_ (3x+2y−14=0)
解2 [(☆)の利用]
2直線①,②の交点を通る直線の方程式は,k を定数として k(8x−2y−19)+2x−6y+9=0 ⋯③ と書ける.これが点 (−2,10) を通るとき, k{8⋅(−2)−2⋅10−19}+2⋅(−2)−6⋅10+9=0 k(−16−20−19)+−4−60+9=0 −55k−55=0 ∴k=−1 従って③より, −(8x−2y−19)+2x−6y+9=0 ∴3x+2y−14=0_

2.5 点と直線の距離
点と直線の距離 点P(x1,y1) と直線 l:ax+by+c=0 の距離 d は,d=|ax1+by1+c|√a2+b2
証明の方針
まず,特別な場合として原点と直線 l の距離を計算する.
↓
一般の点 (x1,y1) との距離は,この点が原点にくるように全体を平行移動して考える.
直線 l:ax+by+c=0 のついて,
[1] 原点と直線の距離 d
原点Oから直線 l に垂線OHを下ろす:
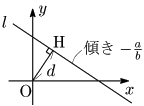
直線OH:bx−ay=0
l と連立して,
H(−aca2+b2, −bca2+b2)
従って2点間の距離の公式により,
d2=(−aca2+b2)2+(−bca2+b2)2=c2a2+b2
d>0 より,d=|c|√a2+b2_
[2] P(x1,y1) と直線の距離 d
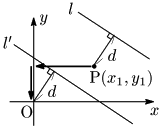
Pが原点にくるように l を平行移動した直線を l′ とすると,
l′:a(x+x1)+b(y+y1)+c=0
∴ax+by+ax1+by1+c=0
よって[1]により,d=|ax1+by1+c|√a2+b2_
(これは[1]のケースを含んでいる.)
■
発展的補足
分子の絶対値は,点と直線の上下関係がはっきりしている場合,外すことができる.(詳しくは「6節 不等式と領域」参照.)
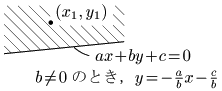
b>0 のとき
① 点が直線の上側
⟺y1>−abx1−cb
⟺ax1+by1+c>0 (∵b>0)
② 点が直線の下側
⟺y1<−abx1−cb
⟺ax1+by1+c<0 (∵b>0)
b<0 のとき
① 点が直線の上側
⟺y1>−abx1−cb
⟺ax1+by1+c<0 (∵b<0)
② 点が直線の下側
⟺y1<−abx1−cb
⟺ax1+by1+c>0 (∵b<0)
例題 点(−4,5) と直線 x−2y+3=0 との距離 d を求めよ.
答
d=|−4−2×5+3|√12+(−2)2=|−11|√5=11√5_

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | [会員] | ||
| 2. 直線の方程式 | [会員] | ||
| 3. 円の方程式 | [会員] | [会員] | |
| 4. 円と直線 | [会員] | [会員] | |
| 5. 軌跡と方程式 | [会員] | [会員] | |
| 6. 不等式と領域 | [会員] |