高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [会員] | |
| 2. 指数関数 | [会員] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

3.1 対数とは
例 y=2x
y=2x の単調性により,
y=1 のとき,x=0
y=2 のとき,x=1
y=4 のとき,x=2
y=8 のとき,x=3
と y の値に対して,x の値がただ1つ定まる.
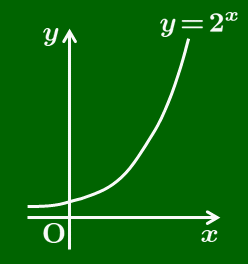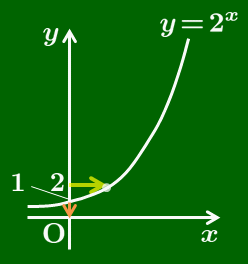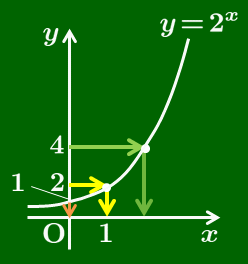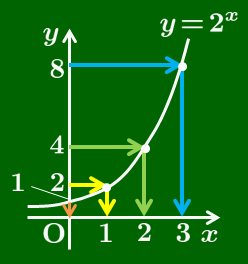
(スライドより抜粋)
そこで,「y=P のとき,P=2x となる x の値」を log2P で表すと, log21=0log22=1log24=2log28=3 となる.
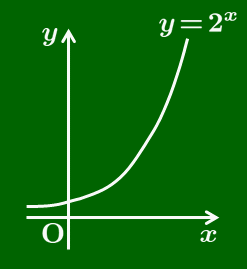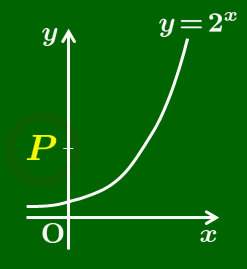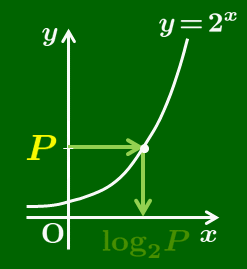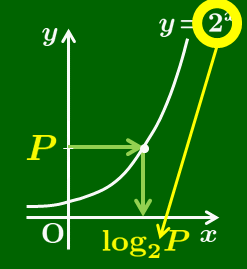
一般に, a>0,a≠1,b>0 のとき,ap=b を満たす p がただ1つ存在し,これを logab と書き,a を底(てい)とする b の対数という.また,b を真数という.
対数 a>0, a≠1, b>0 のとき,ap=b⟺p=logab
補足
対数の底や真数となるための条件
底の条件:正の数であって1ではない
(a>0, a≠1)
真数条件:正の数
(b>0)
例
log381=


log218=



例題 log48 の値を求めよ.
解答例を表示する
3.2 対数の性質
a>0, a≠1 のとき, a0=1, a1=a, , a−1=1a により,次が成り立つ:
loga1=0, logaa=1, loga1a=−1
対数の性質 a>0, a≠1 で,M, Nがともに正の数,kが実数のとき,[1] logaMN=logaM+logaN[2] logaMN=logaM−logaN[3] logaMk=klogaM
証明のポイント
指数法則を利用するため,
すべて □☆ の形に!
r=logaM,s=logaN とおくと, M=ar, N=as である.
[1] MN=aras=ar+s.
(a を (r+s) 乗すると MN)
故に, logaMN=r+s=logaM+logaN
[2] MN=aras=ar−s.
(a を (r−s) 乗すると MN)
故に, logaMN=r−s=logaM−logaN
[3] Mk=(ar)k=akr.
(a を kr 乗すると Mk)
故に, logaMk=kr=klogaM
■

例
log102+log105=log10(2×5) [←性質1]=log1010=1_
log25−log240=log2540 [←性質2]=log218=log22−3=−3_
6log53√5=6log5513=6×13log55 [←性質3]=2_

3.3 底の変換公式
a, b, c が底の条件(正であって1でない)を満たすとする.
logab=p とおくと, b=ap この両辺は正であるから,c を底とする対数をとると, logcb=logcaplogcb=p×logca [←性質3] a≠1 よりlogca≠0 であるから, p=logcblogca p=logab であったから置き換えると,次の底の変換公式と呼ばれる等式が得られる:
logab=logcblogca
またこの式で,c を b とおくと, logab=logbblogba=1logba
即ち,底と真数を入れ替えると,その数の逆数と等しくなる.
底の変換公式 a, b, c が正であって1でないとき(すなわち底の条件を満たすとき),logab=logcblogca 特に,logab=1logba
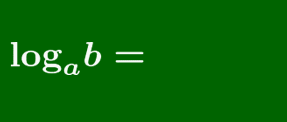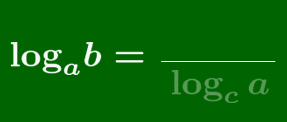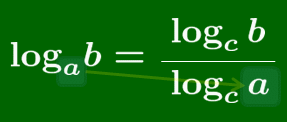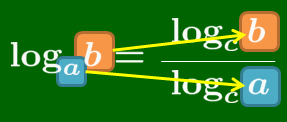
底の変換公式
例
log48=log28log24=32log279=log39log327=23log23×log38=log23×log28log23=log28=3
補足
3番目の例で分かるように,一般に次の関係が成り立つ:
logab×logbc=logac

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [会員] | |
| 2. 指数関数 | [会員] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

