高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [会員] | |
| 2. 指数関数 | [会員] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |

1.指数の拡張
これまでに学んだのは 52 や a4 など,指数部分が自然数であった.例えばこれらは
52=5×5,a4=a×a×a×a
を意味しており,n を自然数として an というのは「a を n 回掛ける」のであった.ここで指数 n を
自然数 → 整数 → 有理数 → 実数
へと拡張することを考える.まずは「自然数 → 整数」の拡張から始めよう.

1.1 0や負の整数の指数
50 や 3-2 は何を意味するのか
a≠0 とする.a0 や a−2 を考えていくのであるが,「a を0回掛ける」や「a を −2 回掛ける」では意味が通らない.ではこれらの数をどのように取り決める(定義する)のがよいだろうか.
a2 から a3 へと指数が1だけ増加すると,数は a 倍された.逆に,a3 から a2 へと指数を1だけ小さくすると,数は 1a 倍される.この規則を a(=a1) から a0 の場合にも適用すると,a1 を 1a 倍したものが a0 だと考えて
a0=a1×1a=1
とするのが自然であろう.更に a0(=1) から a−1 の場合についても
a−1=a0×1a=1×1a=1a
と考えることができる.
a≠0 のとき,
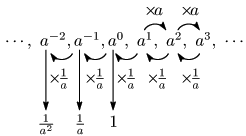
このように考えて,0や負の整数の指数を次のように定義する.
定義 a≠0, n が正の整数のとき,a0=1, a−n=1an, (特に,a−1=1a)
例
(1) 50=1
(2) 3−2=132=19
(3) (−2)−3=1(−2)3=1−8=−18
(4) 0.2−3=(15)−3=1(15)3=53=125

1.2 整数の指数法則
拡張しても指数法則はすべて成り立つ
これまで自然数であった指数を,整数にまで拡張したが,拡張したあとであってもこれまで成り立っていた指数法則はすべて成り立つ.(本当のところは指数法則が成り立つように,0や負の整数の指数を定義したのである.)
a≠0, b≠0 で,m, n が整数のとき,[1] aman=am+n[2] (am)n=amn[3] (ab)n=anbn[4] aman=am−n[5] (ab)n=anbn
例
[1] a2a−3=a2⋅1a3=1a=a−1=a2−3
[2] (a2)−3=1(a2)3=1a6=a−6=a2⋅(−3)
[3] (ab)−2=1(ab)2=1a2b2=a−2b−2

1.3 累乗根
a の n 乗根とは何か
a の n 乗根 n を正の整数とするとき,n 乗して a になる数を
a の n 乗根
という.
a の n 乗根は,方程式 xn=a の解である.
例
9 の2乗根(平方根ともいう)
x2=9 より x2−9=0
∴(x+3)(x−3)=0
よって,3 と −3
8 の3乗根(立方根ともいう)
x3=8 より x3−8=0
∴(x−2)(x2+2x+4)=0
よって,2 と −1+√3i と −1−√3i
−8 の3乗根
x3=−8 より x3+8=0
∴(x+2)(x2−2x+4)=0
よって,−2 と 1+√3i と 1−√3i
16 の4乗根
x4=16 より x4−16=0
∴(x2−4)(x2+4)=0
よって,2 と −2 と 2i と −2i
補足
① 2乗根,3乗根,4乗根,… をまとめて累乗根(るいじょうこん)という.
② 複素数の範囲で考えると,一般に a≠0 のとき,a の n 乗根は n 個ある.(ただし重解も2個,3個,…というように区別して数える.)

1.4 n 乗根 a
「n 乗根 a」と「a の n 乗根」は違うもの
前節で「a の n 乗根」というものを学んだが,これに似た用語に「n 乗根 a」がある.これらは異なるものなので気を付けなければならない.
a の n 乗根について,n が奇数のときと偶数のときで場合分けする.
1.n が奇数のとき
y=x3, y=x5, y=x7, ⋯ といった関数のグラフは,概ね次のような形をしている:
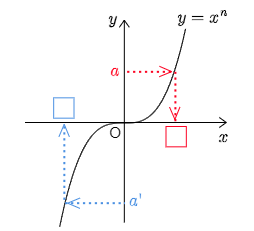
どんな a にも
それに対応する□がただ1つ存在する.
このグラフを見ると,どんな実数 a にも y の値が a となるような実数 x,すなわち xn=a となる x がただ1つだけ存在していることがわかる.この x をn√aと書き表し,「 n 乗根 a 」と読む.
例1 8 の3乗根は,2 と −1±√3i
よって,2 を 3√8 と書き,
「3乗根8」
と読む:
3√8=2
例2 −8 の3乗根は,−2 と 1±√3i
よって,−2 を 3√−8 と書き,
「3乗根−8」
と読む:
3√−8=−2
2.n が偶数のとき
y=x2, y=x4, y=x6, ⋯ といった関数のグラフは,概ね次のような形をしている:
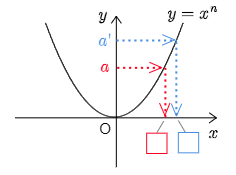
どんな非負の数 a にもそれに対応する
0以上の数□がただ1つ存在する.
このグラフをもとに,y=a のときの x について,a>0, a=0, a<0 に分けて考える.
(i) a>0 のとき
xn=a となる x が正負1個ずつある.その正の方を n√a で表し,「 n 乗根 a 」と読む.そして負の方を −n√a で表し,「 マイナス n 乗根 a 」と読む.
(ii) a=0 のとき
n√0=0
(iii) a<0 のとき
n√a は存在しない.
例 16 の4乗根は,
2 と −2 と 2i と −2i.
よって,
2 を 4√16 と書き「4乗根16」と読む.
−2 を −4√16 と書き「マイナス4乗根16」と読む.
よくある間違い 4√16=±2 (←正しくない.)
まとめ n√a ( n 乗根 a )とは
- n 乗すると a になる数である
- ただ1つの実数である
- n が奇数のとき,a は任意の実数がとれる.
- n が偶数のとき,a≧0 の実数がとれる.
補足
2 乗根 a は,通常左上の 2 を省略する:
2√a → √a
また,「2 乗根 a」や「平方根 a」とは呼ばず,「ルート a」と呼ぶのが通例である.
重要な注意
a>0 のとき,n√a は,その定義から n の偶奇にかかわらず正の数である:
この事実は,次節「1.5 累乗根の性質」で利用される.

1.5 累乗根の性質
√2×√3=√6 といった計算は累乗根でもできる
ここでは n√a の a を正の数に制限する.そうすることで直前の「重要な注意」でも述べたように,n√a は n の偶奇にかかわらず,ただ1つの正の数を表すということがいえる.この事実を用いると,平方根で成り立っていた以下の性質がそのまま一般の累乗根でも成り立つ.
累乗根の性質 a>0, b>0 で,m, n, p が正の整数のとき,
[1] n√(an√(b=n√(ab
[2] n√an√b=n√ab
[3] (n√a)m=n√am
[4] m√n√a=mn√a
[5] n√am=np√amp
証明の方針
[1]~[5]の等式の両辺が,同じ数を指していることを示す.具体的には,A>0 のとき,n√A というのは,
正の数(… ①) かつ n 乗すると A になる(… ②)
を満たすただ1つの実数を意味するのであったから.左辺,右辺のそれぞれについて,①と②の2つを確認すればよい.
※「ただ1つの実数である」という部分は n√A という記号にもともと備わっている.
証明
[1] この等式の右辺である n√ab は,「n 乗すると ab になるただ1つの正の実数」を表しているから,左辺の n√(an√(b も同じ数,すなわち「n 乗すると ab になるただ1つの正の実数」であることを示せばよい.
n√(a>0, n√(b>0 より,n√(an√(b>0.[方針の①]
また,(n√(an√(b)n=(n√(a)n(n√(b)n=ab.[方針の②]
よって,n√(an√(b という数は,
- 正の数 [方針の①]であって,
- n 乗すると ab [方針の②]になる実数
であるから,そのような数はただ1つ n√ab である.よって
n√(an√(b=n√ab
[2] [1] と同様に示される.
[3] n√a>0 より,(n√a)m>0.[方針の①]
また,{(n√a)m}n={(n√a)n}m=am.[方針の②]
よって,(n√a)m という数は,
正の数 [方針の①]であって,
n 乗すると am [方針の②]になる実数
であるから,
(n√a)m=n√am
[4] n√a>0 より,m√n√a>0.[方針の①]
また,
(m√n√a)mn={(m√n√a)m}n=(n√a)n=a.[方針の②]
よって,m√n√a という数は,
正の数 [方針の①]であって,
mn 乗すると a [方針の②]になる実数
であるから,
m√n√a=mn√a
[5] am>0 より,n√am>0.[方針の①]
また,
(n√am)np={(n√am)n}p=(am)p=amp.[方針の②]
よって,n√am という数は,
正の数 [方針の①]であって,
np 乗すると amp [方針の②]になる実数
であるから,
n√am=np√amp
■
例
3√43√54=3√4(3√23√27)(∵[1])=3√83√27(∵[1])=2⋅3=6
(8√9)6=8√96(∵[3])=8√(32)6=8√312=2×4√33×4=2√33(∵[5])=(√3)3(∵[3])=3√3

1.6 有理数の指数
312 は何を意味するか
ここでは指数を有理数にまで拡張することを考える.例えば正の数 a に対して a23 や a−13 といったものがどんな数を表しているとするのがよいのだろうか.その指針となるのが指数法則である.指数が整数の場合の指数法則は次のようなものであった:
復習(整数の指数法則) a≠0 で,m,n が整数のとき, [1] aman=am+n[2] (am)n=amn
いま a を正の数に制限して,これらの指数法則が,m,n が有理数の場合でも成り立つと仮定してみる.例えば
(a23)3=a23×3 (整数の指数法則[2])=a2
といった具合である.すると a23 という数は3乗すると a2 になるから,a23>0 だとすれば3乗根 a2 と考えられる:
a23=3√a2
また,
a13a−13=a13−13 (整数の指数法則[1])=a0=1∴a13a−13=1
よって a13 が0でないとしてこの両辺を a13 で割ると, a−13=1a13
以上のような考察から,有理数の指数を次のように定義する:
定義 a>0 で,m, n が正の整数のとき, amn=n√ama−mn=1amn=1n√am
例
312=√3
534=4√53
813=3√8=2
9−32=1√93=1(√9)3=133=127

1.7 有理数の指数法則
指数法則はいつ何時でも成り立つ
指数を整数にまで拡張していた指数法則であるが,指数を有理数にまで拡張したあとでもそのまますべて成り立つ.
a>0, b>0 で,r, s が有理数のとき,[1] aras=ar+s[2] (ar)s=ars[3] (ab)r=arbr[4] aras=ar−s[5] (ab)r=arbr
例
816×832=816+32=853={(23)53=25=323√85=(3√8)5=25=32
16−12={(42)−12=4−1=1411612=1√16=14
a>0 のとき,
√a×6√a÷3√a2=a12×a16÷a23=a12+16−23=a0=1

1.8 無理数の指数
2√2 は何を意味するか
例 2√2(=21.41421356⋯)
√2 は無理数,すなわち循環しない無限小数で,いつまでも不規則な数字の列が続く.しかし,どこかで小数を打ち切って有限小数にしてしまえば,有限小数はどんなものでも分数の形に表現し直すことができるから有理数である.従って,それらを2の指数部分にのせたときには1つ値が定まる.例えば,1.41は 141100 であるから,
21.41=2141100=100√2141
である.このようにして,√2 の小数部分を1桁ずつ止めながら位を増やしていくと,次のような数の列が得られる:
21, 21.4, 21.41, 21.414, 21.4142, 21.41421, ⋯
これら1つ1つの数は指数部分が有理数であるから値が定まる.より具体的には次のような数の列になる:
21=221.4=2.63901⋯21.41=2.65737⋯21.414=2.66474⋯21.4142=2.66511⋯21.41421=2.66513⋯⋮
この数の列は,小数部分を増やしていくと,どんどん一定の値に近付いていく.その限りなく近付く先の値をもって,2√2 の値とするのである.
2√2=2.6651441426⋯
補足
指数を無理数にまで拡張したので,a>0 のとき,任意の実数 x で ax の値が定められた.つまり指数部分を
自然数 → 整数 → 有理数 → 実数
へと拡張する作業がここに完了した.
1.2節 で登場したすべての指数法則は,指数が実数になっても成り立つ.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第5章 指数関数・対数関数
| スライド | ノート | |
| 1. 指数の拡張 | [会員] | |
| 2. 指数関数 | [会員] | |
| 3. 対数とその性質 | [会員] | |
| 4. 対数関数 | [会員] | |
| 5. 常用対数 | [会員] |